Клод Шеннон

Голодный нуждается в хлебе, насытившись – ищет зрелищ. Для сытых греки придумали театр, а египтяне – искусство жонглирования. По-видимому, египтянам развлечения понадобились раньше. Во всяком случае, первое документальное свидетельство относится к концу Среднего Царства, между 1994 и 1781 гг. до Р.Х. Это – изображение группы женщин, жонглирующих шарами. Найдено оно в захоронении не установленной царственной особы [1].
Сытый и отдохнувший, человек оглядывается вокруг и размышляет, чем бы заняться «для души». Как предмет изучения, жонглирование ничем не хуже прочих объектов. Первая мысль: как бы так научиться – самому ловко подбрасывать мячики? Оказывается – требуется длительная тренировка. Что ж, тогда – во-вторых: нельзя ли столь однообразную, но технически сложную работу поручить механизмам? Наконец, третье явно вытекает из предыдущего: нужна математическая модель процесса.
Вволю позанимавшись первым и вторым, человек перешел к третьему. В 1903 г. появилось первое математическое исследование, посвященное жонглированию. Позднее, в 1970-е, Massachusetts Institute of Technology (MIT) на свет произвели жонглирующего робота. Разработал устройство Клод Шеннон (Claude Elwood Shannon), подкрепив физическую модель простой внешне формулой, известной как теорема жонглирования Шеннона: (F + D) H = (V + D) N, где F – время свободного полета шарика, D – время его нахождения в руке, V – время, пока руки свободны, N – число шаров, H – количество рук.
Шеннон и сам умел жонглировать, - тремя шарами, да еще балансируя при этом на одноколесном велосипеде, им же самим сконструированном. Говорят, за этим занятием его иногда можно было встретить в коридорах MIT. Возможно, это просто байка, какие во множестве рассказывают об известных и неординарных личностях. Напротив, D.Slepian из Bell Lab отмечает [2] постоянную сосредоточенность своего маститого коллеги на работе: «Многие из нас приносили ланчи из дома и совмещали поглощение еды с математическими играми, используя доску на стене. Но не Шеннон – он продолжал работать за закрытой дверью. Однако стоило вам зайти – и вас встречали вполне терпеливо, с готовностью помочь. Суть задачи он схватывал моментально. Он был настоящим гением, единственным из моих знакомых, к кому я могу применить такое определение».
Так, juggling a bit*, сделать Шеннон успел за свою жизнь очень не мало. Наверное, способность быстро ориентироваться в окружающей среде и природный ум взаимно дополняли друг друга.
Вряд ли можно говорить здесь о прямом влиянии родителей, хотя факт их высокой образованности сомнению не подлежит. Отец Клода занимал должность судьи в Гейлорде, маленьком городке американского штата Мичиган, а мать возглавляла там же среднюю школу. Но вот на деда, фермера и изобретателя, обратить внимание стоит. Среди конструкций деда – посудомоечная машина и ряд механизмов сельскохозяйственного назначения. Между прочим, биографы отмечают также дальше родство Шеннона с выдающимся изобретателем Томасом Эдисоном [3]. Родился Клод Шеннон 30 апреля 1916 г. В часы, свободные от занятий в Gaylord High School, он успевал работать посыльным в Western Union. Но это не мешало совершенствованию в математике и инженерии. Интерес к ним проявился в юноше рано, и в дальнейшем оба предмета равно привлекали его. Недаром, заканчивая в 1936 г. Мичиганский университет, он получил бакалаврские степени сразу по двум дисциплинам, математике и электротехнике. Для продолжения учебы Клод отправился в Массачусетский технологический институт. Деканом тамошнего инженерного факультета был В.Буш (Vannevar Bush, 1890-1974). В то время как некоторые исследователи уже активно вели разработки цифрового компьютера, Буш занимался воплощением в жизнь классической идеи дифференциальной машины Чарльза Бэббиджа. Шеннон, по примеру многих американских студентов, совмещал учебу с временной работой. В MIT оба занятия, благодаря Бушу, удачно совмещались. Личность руководителя этого проекта Буша занимает особое место в истории американской науки, и вот почему. Спустя несколько лет после описываемых нами событий была развязана Вторая мировая война. В июне 1940 г. Буш встретился с президентом США Рузвельтом и изложил план активизации научных разработок военного назначения и необходимых мер государственной поддержки [4]. Координацию деятельности всех привлекаемых сторон и ресурсов должна была осуществлять новая структура – National Defense Research Committee (NDRC). Предложение Буша было одобрено, и он же стал председателем этого комитета, получив прямой выход на Белый Дом. Уже в середине 1941 г. Появилась еще одна организация, финансируемая по линии Конгресса, - The Office of Scientific Research and Development (Управление научных исследований и разработок, OSRD). В конце концов, NDRC подчинили OSRD как одно из подразделений последнего, а Буш был назначен его директором. К концу войны OSRD стал ведущей исследовательской организацией в военной сфере. Множество важнейших, секретных в то время, разработок оказались связаны с его деятельность и, естественно, курировались Бушем. Достаточно упомянуть лишь одну, пожалуй, самую известную из них, - «Манхэттенский проект» по созданию первой атомной бомбы. Естественная закрытость от общества деятельности OSRD не мешала известности Буша, которого в 1942 г. журнал «Colliers» охарактеризовал как «человека, который может выиграть или проиграть войну». Таков был административный потенциал этого ученого, фактически реформировавшего всю систему государственной и общественной поддержки науки в США.
Хороший администратор должен обладать даром предвидения. Хороший ученый – точно так же. В лице Буша счастливо сочетались обе ипостаси. В 1945 г. в журнале «The Atlantic Monthly» появилась его статья «As We May Think» («Как мы предполагаем»), которую спустя два месяца перепечатал «Life». Идеи Буша вызвали широкий резонанс. По сути, он описывал машину для хранения и обработки информации, названную «Memex». Функционально та машина очень напоминала современный гипертекст, что признает и сам Ted Nelson, предложивший этот термин в 1960-х годах [4].
Но вернемся в 30-е, в MIT. Конечно, с современной точки зрения, аналоговая машина, обеспечению функционирования которой Шеннон посвящал свое рабочее время под руководством Буша, выглядит эдаким монстром. За исключением электромоторов, все остальные узлы были механическими. Тем не менее, сия шумно бряцающая шестернями и приводами конструкция, получившая известность под именем «дифференциального анализатора», успешно справлялась с решением обыкновенных дифференциальных уравнений высоких порядков. Ввод параметров очередного уравнения занимал от двух до трех дней, процесс решения – не менее того. Если же менялась постановка задачи, то машину следовало разобрать на части и вновь собрать в новой конфигурации [5]. Не для того ли нужна была «рабочая сила» в лице будущего создателя теории информации?
Какова роль зубчатых колес? Их сочленения воспроизводят передаточные числа, необходимые при вычислениях в десятичной нумерации. В двоичной системе счисления «зубьев» понадобится меньше, правда шестеренок – гораздо больше. Но можно обойтись и другими составляющими конструкции!
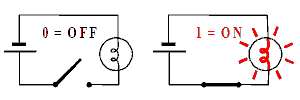
Для начала (1938 г.) Шеннон защитил магистерскую диссертацию по электротехнике – на тему «A Symbolic Analysis of Relay and Switching Circuits» («Символьный анализ цепей с реле и переключателями»). В этой работе, положившей начало современной теории переключательных схем, он продемонстрировал, как применение аппарата булевой алгебры помогает их оптимизировать. Нужно ли добавлять, что рабочий алфавит включает лишь два символа – 0 и 1? Много позднее профессор H.Gardner из Гарвардского университета отозвался об этой работе как о «возможно самой важной и, одновременно, самой знаменитой магистерской диссертации столетия» [5]. Но и тогда ее значимость была высоко оценена научным сообществом: автору присудили престижную премию для молодых ученых (до 30 лет) за лучшую работу года в области инженерных дисциплин.
Еще два года спустя, в том же MIT, Шеннон получил степень PhD по математике. Очевидно, уровень требований, предъявляемых там к соискателю, был достаточно высок. Во всяком случае, Клоду пришлось, занимаясь языковой подготовкой, нанять педагогов по французскому и испанскому языкам, а экзамен по немецкому он сдавал дважды [3]. Темой докторской диссертации с подачи Буша стала генетика популяций – «An algebra for theoretical genetics». Так случилось, что для специалистов в этой области тогда работа осталась неизвестной, опубликовали ее лишь в 1993 г., в сборнике избранных трудов Шеннона. Сам он больше к вопросам генетики не обращался [6].
В качестве национального стипендиата Шеннон провел академический 1940-41 год в Принстоне, работая под руководством известного математика Германа Вейля [5]. После чего на долгие годы, вплоть до 1972, обосновался в Bell Telephone Laboratories в штате Нью-Джерси. Там его давно знали, ведь летние месяцы, свободные от учебы в MIT, молодой ученый стажировался у них. Группа, в которую он попал, занималась разработкой эффективных методов передачи информации и повышения надежности протяженных телефонных и телеграфных линий. Да и, собственно, сама Bell Labs возникла в связи с подобными техническими задачами, выделившись в 1925 г. из AT&T в качестве исследовательского подразделения.
За десятилетия существования Bell Labs ее сотрудники немало преуспели, пополняя копилку достижений, в которой собрано множество самых разных разработок, оцененных, в том числе, шестью Нобелевскими премиями по физике [7]. Не забывали там и о компьютерных приложениях, достаточно упомянуть хотя бы одноразрядный сумматор, язык C и операционную систему UNIX. Как с юмором замечает Ч.Петцольд [8], «фирма Bell Labs в течение многих лет была местом, где умные люди могли заниматься почти всем, что их интересовало. Некоторых из них, к счастью, интересовали компьютеры».
Увлеченность «некоторых» сотрудников явно простиралась за рамки рабочего времени. Тот самый двоичный полусумматор Джордж Стибиц (George Stibitz, 1904-1995) [9] собрал почему-то не на работе, а дома, на кухонном столе (случилось это в 1837 г.). С легкой руки жены ученого, устройство нарекли эффектным именем «кухонная машина» («Model K» – от kitchen, кухня). Готовый прототип Стибиц принес на работу, а спустя два года (1939, совместно с коллегой, чье имя Samuel Williams) представил вычислительную машину – «Complex Number Calculator», которая выполняла уже все арифметические операции, причем с комплексными числами. Широкую известность этот электромеханический вычислитель получил как «Bell Labs Model Relay Computer», и некоторые источники называют его первым в данном классе. Классифицирующий термин «электромеханический» означает, что основу его логического устройства составляли релейные схемы.
Вообще говоря, выяснение приоритетов в этой научно-технической области, где идеи в 1930-е годы буквально носились в воздухе, — задача неблагодарная. Известны даже случаи судебных разбирательств, например, иск Дж.Атанасова (John Atanasoff, 1903-1995), оспаривавшего патент компании-разработчика компьютера ENIAC. Достойны упоминания здесь и труды немецкого ученого К.Цузе (Konrad Zuse, 1910-1995). Не имея ни малейшего представления о работах заокеанских коллег, по времени он несколько опередил американцев, завершив сборку прототипа своего компьютера в 1938 г. [8,9]. Однако долголетняя закрытость германских архивов привела к тому, что широкую известность в научном мире его машина Z1 обрела лишь десятилетия спустя.
Занятным выглядит следующее совпадение. Цузе, как и Стибиц, тоже конструировал свою машину дома, только не на кухонном столе, а в гостиной берлинской квартиры родителей. Если вспомнить еще более поздние примеры – С.Возняка и С.Джобса, обосновавшихся в гараже [10], плюс к тому Линуса Торвальдса, долгие месяцы наращивавшего Linux тоже в домашней тиши [11], — то напрашивается вывод: лучшие компьютерщики – большие домоседы.
Но вернемся вновь в Bell Labs. Мы уже упоминали о тематике исследований группы, в которую включился Шеннон. В военное время появились специфические задачи, в частности, анализ целей вражеских самолетов и ракет. Результаты этой работы оказались особенно актуальными в связи с массированными бомбардировками Англии [3]. Самого же Клода интересовали также возможности защиты передаваемой информации от «несанкционированного чтения». В 1945 г. он подготовил закрытый отчет, посвященный математическим аспектам криптографии [6]. В открытой печати переработанную версию стало возможным опубликовать лишь после войны: в 1949 г. Журнал «Bell System Technical Journal» (BSTJ) поместил на своих страницах статью «Communication theory of secrecy systems». Принято считать, что именно эта работа перевела криптографию из категории искусства в лоно науки.
Стоит отметить, что в обсуждении криптографических проблем у Шеннона были достойные собеседники. Для решения одной из задач в Bell Labs из Англии специально приезжал Алан Тьюринг [12]. Речь шла об изготовлении шифрующего телефонного устройства для обеспечения регулярных переговоров Рузвельта с Черчиллем, разделенных Атлантикой.
Исследования Шеннона в области защиты данных базировались на новом подходе к оценке количества информации, нашедшем отражение в его весьма обширной по объему и ставшей основополагающей для многих направлений статье «Математическая теория связи» (1948) [13]. В своей теории Шеннон отталкивался от двух известных к тому времени результатов.
Первый из них принадлежал Х.Найквисту (Harry Nyquist, 1889-1876), шведу по национальности, эмигрировавшему в США в 1906 г. Получив в 1917 г. степень PhD в Йельском университете, следующие 17 лет он работал в AT&T [14]. В контексте нашего обсуждения интерес представляют две публикации, посвященные технике связи: «Certain Factors Affecting Telegraph Speed» (в уже знакомом нам журнале BSTJ за 1924 г.) и «Certain Topics in Telegraph Transmission Theory» (A.I.E.E. Trans., v. 47, 1928). Найквист установил, что обратимая дискретизация аналогового сигнала возможна, если использовать частоту дискретизации, превышающую наибольшую из частот компонент, по крайней мере, вдвое.
Шеннон имел возможность не только познакомиться с публикацией, но и общаться с ее автором в стенах Bell Labs, где Найквист работал с 1934 г. вплоть до ухода на пенсию в 1954 г. Шеннону «оставалось» лишь формально обосновать вывод коллеги. Ныне этот результат известен как «теорема отсчетов» Найквиста-Шеннона.
Второй же результат напротив, подвергся ревизии. Американский инженер-связист R.Hartley ввел (BSTJ, July 1928) числовую характеристику для оценки меры неопределенности опыта. Шеннон воспользовался идеей Хартли применить логарифмическую шкалу, но в своей формуле связал ее с вероятностным подходом (см. подробное обсуждение в [15]). Математическое выражение совпало с формулой для энтропии – понятия, введенного австрийским физиком Больцманом (L.Boltzmann. 1844-1906) еще в XIX веке. Название было позаимствовано и закреплено в теории Шеннона за средним количеством информации, приходящейся на один знак для данного источника сообщений. Поскольку знаки берутся из двоичного алфавита, то единицей измерения следует считать двоичный разряд.
Следую предложению своего коллеги Тьюки**, Шеннон принял хорошо нам знакомый термин bit (от binary digit). Однако последователи автора теории информации сочли правильным отметить его заслуги введением альтернативного названия для единицы измерения – 1 Sh (shannon) [16]. Если сообщение состоит из M Sh, то его можно закодировать, используя ровно столько же битов.
К сожалению, на практике лишь в исключительных случаях удается точно оценить количество информации и, соответственно, применить идеальную схему кодирования. В большинстве случаев применяется кодирование избыточное. В той же работе Шеннон обратил внимание на значительную избыточность естественного языка, дав мощный толчок многочисленным исследованиям математиков-лингвистов на эту тему.
Для уменьшения избыточности информации при передаче ее по каналам связи Шеннон предложил метод, известный ныне как алгоритм Шеннона-Фано (R.M.Fano). Далее Шеннон обсуждает проблему борьбы с помехами канала, и оказывается, что избыточность информации можно обратить на борьбу с ее искажениями. Здесь он указывает на возможности защитного кодирования и приводит механизм, только что предложенный Хэммингом. Вы уже догадываетесь, где Шеннон мог общаться с Хэммингом***?
Интенсивные научные занятия Клода Шеннона не мешали ему оставаться жизнелюбом. В стенах Bell Labs он познакомился с вычислителем-аналитиком Mary Elizabeth 'Betty' Moore, ставшей его женой в 1949 г. [3]. Впоследствии у них родилось трое детей.
В том же году Шеннон направил Американскому институту инженеров доклад (статья опубликована в 1950 г.), посвященный проблеме создания искусственного интеллекта. В качестве «экспериментальной площадки» рассматривалась шахматная игра, с легкой руки Шеннона принявшая на себя эту роль на многие десятилетия.
Для формализации игры Шеннон предлагал два альтернативных механизма: полный перебор фиксированной глубины (метод «грубой силы»), либо выборочный перебор. Однако четких рекомендаций для второго подхода он не дал. Причина, по мнению М.Ботвинника****, в том, что «Шеннон познакомился с шахматами лишь в возрасте 28 лет, шахматным специалистом он не был» [17].
Отойдя от шахматной карьеры, Ботвинник серьезно занялся созданием шахматной программы, основанной на алгоритме, который имел много общего со вторым механизмом. Вот что он рассказывает о своей личной встрече с американским ученым. в 1960 г. Ботвинник прочел в Университете им. Гумбольдта в Берлине лекцию «Люди и машины за шахматной доской». С ее публикацией, как выяснилось, познакомился и Шеннон. Весной 1965 г. всемирно известный профессор приехал в Москву и пожелал встретиться с Ботвинником. При встрече «мы обсудили проблему создания искусственного шахматиста. В заключение Шеннон предложил сыграть партию, а по ее окончании попросил какой-нибудь сувенир. Я тут же восстановил текст партии и вручил своему партнеру на память» [17].
Мы уже отметили, что шахматное программирование стало полигоном для новой области приложения компьютерных технологий – решения задач управления. По словам Ботвинника, «престиж автора теории информации Шеннон столь велик, что его статья незамедлительно положила начало новому научному направлению», решению неточных переборных задач.
Насколько Шеннон оказался провидцем? Судите сами. В 1966-67 гг. состоялся заочный шахматный матч между «искусственными шахматистами». Соперничали в нем, с одной стороны, программа Московского института теоретической и экспериментальной физики, установленная на сравнительно маломощной отечественной машине, с другой – программа Стэнфордского университета, использовавшая мощный американский компьютер. Окончательный счет 3:1 в пользу Москвы. На этом фоне странным кажется то обстоятельство, что московская программа, в основном, «исповедовала» первый принцип Шеннона, а продвинутый алгоритм американской программы был составлен в согласии со вторым подходом. Причину конечного результата Ботвинник усматривает [18] в том, что «реализация первого принципа достаточно проста, а как реализовать второй - было неведомо. Конкретное решение (правило отбрасывания ходов), примененное американским математиком Маккарти, оказалось неудачным».
Прошло несколько десятилетий. Второй подход не принес больших успехов ни в шахматном программировании, ни в решении задач управления, которые требуют изощренных эвристик для сокращения перебора. А вот компьютерное программирование по первому принципу Шеннона процветает. За счет чего? Благодаря бурному развитию технологий, ушедших далеко вперед. Удается обеспечить такую глубину дерева перебора, что программа, установленная на многопроцессорной машине, обыгрывает любого – как теперь пишут, «белкового» — шахматиста, включая чемпиона мира.
Тем временем признание заслуг Шеннона росло. В 1956 г. его вновь привлек к преподаванию MIT, президентом которого в 1957 г. стал Буш. Семья Шеннона поселилась поблизости от MIT, почетным профессором которого Шеннон стал в 1978 г. Ему присуждались десятки почетных наград. Дюжина крупнейших университетов и академий мира удостоили Шеннона почетных степеней и званий.
Круг его интересов простирался от конструирования электромеханической мыши, самостоятельно выбирающейся из лабиринта, до искусственного шахматиста, от создания одноколесного велосипеда со смещенным балансом до теории информации, от оптимизации портфеля инвестиций участника фондового рынка до странного механизма под названием Ultimate Machine [19].
Название этого агрегата можно перевести и как «первичная машина». Это был ящик внушительных размеров с рубильником на стенке. Стоило кому-то повернуть его, как конструкция начинала трястись и шуметь. Затем из ее чрева вытягивалась рука, которая поворачивала тумблер назад, выключая машину. На вопрос, зачем Шеннон соорудил эту машину, он отвечал, что хотел лишь посмотреть на реакцию свидетелей столь необычного зрелища.
Вот еще история, поведанная сами Шенноном и иллюстрирующая одновременно присущее ему чувство юмора и самокритичность [20]. Однажды во время его лекции по математике в Принстоне задняя дверь в аудиторию тихонько отворилась, и в нее протиснулся Альберт Эйнштейн. Он постоял некоторое время, а потом что-то прошептал на ухо одному из слушателей из дальнего ряда, после чего так же незаметно удалился. По окончании лекции Шеннон поспешил отыскать собеседника Эйнштейна, сгорая от любопытства, как отозвался великий человек о его работе. Ответом было: Эйнштейн выяснял, где находится мужская комната.
В 1978 г. Шеннон отошел от дел. Через несколько лет он нежданно «объявился» на некоем симпозиуме. Один из участников вспоминал, что эффект был равнозначен тому, «как если бы Исаак Ньютон появился на конференции по физике». Когда присутствующие узнали Шеннона, его немедленно втащили на сцену. Произнеся короткую речь, он немного пожонглировал, после чего долго давал автографы выстроившейся очереди [20].
В начале 1990-х годов у Шеннона появились симптомы болезни Альцгеймера. Когда в 1998 г. комплекс из двух зданий AT&T в Нью-Джерси, где долгие годы в Bell Labs работал Шеннон, получил имя Shannon Laboratory. Сам он вряд ли осознавал это. Болезнь сделала свое дело, к тому времени Шеннон уже мало кого узнавал. В октябре 2000 г. в присутствии жены Шеннона, Бетти, Общество теории информации IEEE открыло в Гейлорде, родном городе Шеннона, его скульптурный портрет [6]. Умер Шеннон в 2001 г., в возрасте 84 лет.
В большом доме Шеннонов осталась игровая комната. Вокруг на стендах - комплекты расставленных шахмат и огромный барабан, механическая мышь в лабиринте и рулетка, булавы и несколько глобусов. Тут же фигуры самых разных клоунов и даже отдельная диорама с ними. Клоуны умеют жонглировать.
Столяр С.Е.
* Жонглируя понемногу
** John Wilder Tukey (1915-2000). С 1945 г. Тьюки, признанный математик-статистик, совмещал работу в Принстоне и Bell Labs [2].
*** Richard Wesley Hamming (1915-1998). Крупный математик компьютерщик Ричард Хэмминг работал в Bell Labs с 1946 по 1976 г. [2].
**** Михаил Моисеевич Ботвинник (1911-1995), шестой чемпион мира по шахматам, д-р технических наук.
Использованные источники
1. http://www.juggling.org/
2. http://www-history.mcs.st-andrews.ac.uk/history/
3. http://web.mit.edu/newsoffice/nr/2001/shannon.html
4. http://ibiblio.org/pioneers/bush.html
5. http://scienceworld.wolfram.com/biography/Shannon.html
6. Notices of the AMS, Vol. 49, Num. 1. - January 2002.
7. http://www.bell-labs.com/about/awards.html
8. Петцольд Ч. Код. М.: издательско-торговый дом "Русская Редакция", 2001
9. http://www.home.gil.com.au/~bredshaw/
10. http://unix.org.ua/press/skpress/RESELLRA/14/13.htm
11. Даймонд Д., Торвальдс Л. Just for FUN. рассказ нечаянного революционера. М.: ЭКС-МО, 2002
12. http://www.advogato.org/article/251.html
13. A Mathematical Theory of Communication, BSTJ. Vol. 27, 1948. (Перевод в сборнике избранных работ Шеннона: Работы по теории информации и кибернетике. М.: ИЛ, 1963. С. 243-322.)
14. http://en.wikipedia.org/wiki/Harry_Nyquist
15. Яглом А.М., Яглом И.М. Вероятность и информация. Изд. 3-е, перераб. и доп. М.: Наука, 1973.
16. http://www.unc.edu/~rowlett/units/dictS.html
17. Ботвинник М.М. От шахматиста - к машине. М.: Физкультура и спорт, 1979.
18. Ботвинник М.М. Алгоритм игры в шахматы. М.: Наука, 1968.
19. http://www.stanford.edu/~vjsriniv/project/ai.html
20. http://www2.bc.edu/~lewbel/Shannon.html
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Отличная статья! Самая интересная о Клоде Шенноне из всех которые я читала. Спасибо!
Спасибо. Интересная статья
Еще немного про Шеннона, жонглирование и квантовую физику:
http://kniganews.org/map/n/00-01/hex1f/
и
http://kniganews.org/2012/12/25/beyond-clouds-33/