Человеческие пределы в жонглировании
Вступление от переводчика
Ниже приведен перевод статьи Джека Кальвана (Jack Kalvan) "Человеческие пределы. Каким максимальным количеством предметов можно жонглировать" (оригинал статьи можно прочитать здесь). Статья датируется 1997 годом (24 июля, если быть более точным). На данный момент некоторые рекорды, указанные в статье, устарели. Тем не менее, само исследование и его результаты, на мой взгляд, актуальности не потеряли. В любом случае, интересно сравнить прогнозы многолетней давности с текущими данными. Прочие исследования и текущие (на момент написания перевода) рекорды будут представлены в конце.
Человеческие пределы
Каким максимальным количеством предметов можно жонглировать
Не хотелось бы никого расстраивать, но ни один человек не сможет жонглировать 100 мячей. Очень мало людей достигли уровня, чтобы выбросить одиннадцать или двенадцать предметов в воздух, и не более чем на несколько секунд. Никто даже не приблизился к 13 мячам. Но действительно ли это предел человеческих возможностей?
Скорость рук - один из основных факторов, ограничивающих количество объектов, которым можно жонглировать. (Другими важными факторами являются точность бросков, достаточно длинные руки и наличие достаточного пространства в воздухе для жонглирования.) Я решил выяснить, есть ли у кого-нибудь скорость рук, необходимая для жонглирования 13ю или более мячами. Поэтому я разработал эксперимент для измерения теоретических пределов человеческого жонглирования - с учетом ускорения рук.
Чтобы записать нужные уравнения, введем следующие переменные:
- b = число мячей
- h = число рук
- f = время полета мяча, от броска до кетча)
- τ = время между двумя бросками из одной руки.
- Vv = вертикальная скорость броска
- g = ускорение свободного падения (~ 9.81 м/с2)
- r = "коэффициент задержки" или доля времени, в течении которого рука держит мяч. Мои тесты показывают, что r обычно составляет около 2/3.
- Ω = среднее количество мячей находящихся в воздухе, приходящихся на одну дугу.
r также можно представить как среднее количество мячей в руке во время жонглирования. А Ω может быть выражена как количество мячей приходящихся на одну руку минус количество мячей в руке: Ω = (b / h) - r .
Ω также равна времени, которое мячи проводят в полете, поделенное на частоту кетчей: Ω = f / τ .
Для упрощения расчетов я буду считать, что мячи бросаются и ловятся на одной высоте. Ньютоновская физика говорит нам, что время полета мяча, f = 2 Vv / g. Подставляя это выражение для f во второе уравнение для Ω, получаем Ω = 2 Vv / g / τ
Поскольку g является константой, очевидно, что Ω пропорционально скорости броска руки, деленной на время между бросками. Это означает, что количество мячей в воздухе при жонглировании тесно связано с ускорением руки. Хотя руки жонглера не обязательно разгоняются плавно, количество мячей, которое можно выбросить в воздух, примерно пропорционально максимальному ускорению рук.
Я подумал, что если я измерю максимальное ускорение рук жонглера простым акселерометром, я смогу примерно рассчитать максимальное значение Ω. Подставив полученное значение в уравнение b / h = Ω + r получим приблизительное максимальное количество мячей, которым теоретически можно жонглировать. Помним, что максимальное количество мячей рассчитывается только из скорости, с которой жонглер может потенциально бросать мячи в воздух. При этом не учитывается точность бросков и возможность столкновений.
Поскольку количество жонглируемых мячей пропорционально ускорению руки, следовательно, высота жонглирования не связана с ускорением руки. Например, если вы жонглируете 5 мячами высоко, у вас будет примерно такое же ускорение руки, как если бы вы жонглировали низко. Разница в том, что для высокого жонглирования вы ускоряетесь в течении более длительного времени и, следовательно, имеете большее движение рук и более высокую скорость броска.
Я считаю, что следующая таблица показывает, как производные вертикального движения руки относятся к жонглированию:
| Y | Позиция руки | определяет где происходит жонглирование |
| dY/dt | Скорость руки | определяет как высоко можно бросить |
| d2Y/dt2 | Ускорение руки | определяет каким количеством можно жонглировать |
| d3Y/dt3 | Рывок руки (Hand jerk) | определяет насколько высоко можно жонглировать заданным числом мячей |
| d4Y/dt4 | Тряска руки (Hand snap) | определяет насколько плавно можно жонглировать заданным числом мячей на заданной высоте |
Жонглерометр (Jugglemeter)
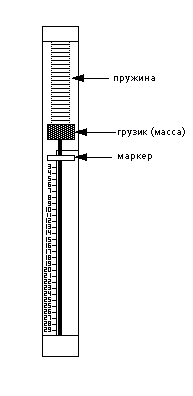
Этот простой прибор измеряет ускорение руки. Небольшая масса соединена с пружиной внутри трубки. Когда рука ускоряет устройство (встряхивая его вверх и вниз), на массу действуют две противоположные силы: сила ускорения (сила = масса * ускорение) и сила пружины (сила = жесткость пружины * расстояние растяжения). Эти силы находятся в равновесии при растяжении пружины. Маркер отмечает максимальное расстояние, на которое была растянута пружина.
Поскольку масса и жесткость пружины постоянны, максимальное ускорение пропорционально расстоянию растяжения. А следовательно расстояние, на которое пружина растягивается, будет пропорционально потенциально жонглируемому количеству мячей.
Калибровка Жонглерометра
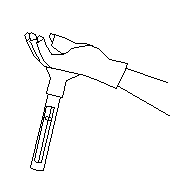
Чтобы откалибровать прибор, я прикрепил его к задней части перчаток. Такой метод неплохо работал с небольшим числом мячей, но перчатка и вес жонглерометра затрудняли жонглирование. К тому же неидеальное жонглирование приводило к искусственно завышенным показаниям, поскольку для кетчей неточных бросков требовалось большее ускорение.
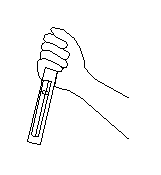
Чтобы откалибровать и проверить жонглерометр на большем числе мячей, я обнаружил, что проще всего сначала жонглировать несколькими мячами достаточно долго, чтобы прочувствовать процесс. Затем я отбрасывал мячи, поднимал жонглерометр и воспроизводил одно и то же движение руки, удерживая его. Подобный процесс не является очень точным, поскольку опирается на способность воспроизводить движение руки как при жонглировании, но с вычетом мячей. Тем не менее, после тестов с большим количеством жонглеров и до 10 мячей, и экстраполируя результаты, я убежден, что ошибка калибровки составляется менее 10%.
Каждый жонглер, которого я тестировал, повторял калибровочный тест с тем количеством мячей, которым они могли свободно жонглировать, чтобы удостовериться, что калибровка была довольно точной. Некоторые люди не смогли имитировать правильное движение руки без собственно жонглирования мячами. С другой стороны, многие смогли воспроизвести правильное движение руки, и, сделав вид, что жонглируют 5ю мячами, были шокированы, увидев показание счетчика "5". "Откуда ему это известно?!!"
Чтобы найти максимальный потенциал каждого субъекта/подопытного, я сказал им встряхивать жонглерометр так сильно и быстро, как только они могут, в течении нескольких секунд, вверх и вниз. (Это была самая интересная часть для наблюдателей.) Я измерил максимум на каждой руке и давал еще одну попытку, если они думали, что могут сделать лучше.
Суммируя результаты теста
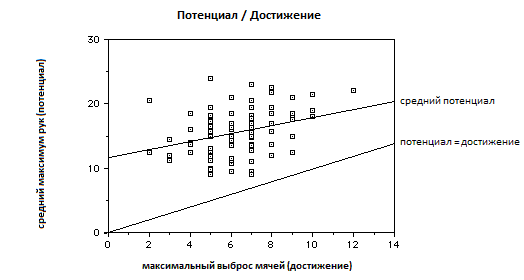
Я протестировал более 100 человек, начиная от не-жонглеров до некоторых из лучших жонглеров в мире. Каждый из испытуемых имел скорость рук достаточную для жонглирования 9 мячами. Средний показатель составил 16 мячей, а максимальный - около 24. Скорость рук, как правило, несколько увеличивалась с уровнем жонглирования. Те, кто говорил, что они могут сделать выброс 9 или более мячами, показывали средний результат около 18,3, в то время как у тех, кто никогда не выбрасывал 5 мячей, средний результат составил около 14,4.
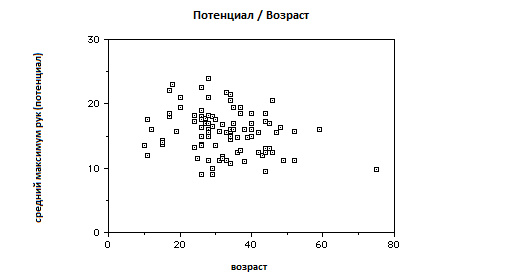
Сравнение испытуемых с сопоставимыми способностями к жонглированию: средняя скорость рук была самой высокой для людей в возрасте около 18 лет; наблюдалось небольшое снижение скорости рук с возрастом; мужчины, как правило, получали несколько более высокие показатели, чем женщины.
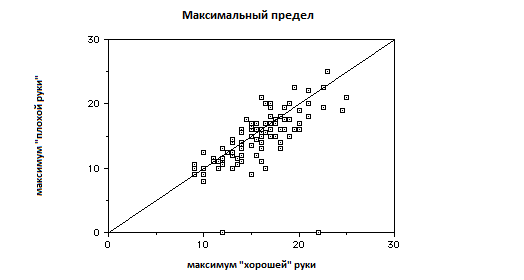
Часто наблюдалась разница между двумя руками, и многие были удивлены, обнаружив что получили лучший результат на "плохой" руке.
Я подозреваю, что некоторые испытуемые не старались изо всех сил. Также я подозреваю, что некоторые могли бы показать лучший результат, больше расслабив руки - это помогло мне.
Заключение
Каждый протестированый человек продемонстрировал ускорение руки достаточное для плавного жонглирования 9ю мячами. К сожалению, кетчи кривых бросков в беспорядочном, неаккуратном каскаде 9ю мячами требуют намного большего ускорения. И только некоторые из протестированных обладали точностью для плавного жонглирования 9ю мячами.
С практикой, точность улучшается, требования к ускорению уменьшаются, а жонглирование требует все меньше и меньше усилий. Требуется гораздо меньше усилий, чтобы хорошо жонглировать 7 мячами, чем плохо жонглировать 7 мячами.
Попробую показать, как неточность приводит к большему ускорению. Если сделать один бросок слишком далеко и приходиться переместить ловящую руку в два раза больше обычного горизонтального расстояния за тот же промежуток времени, это потребует вдвое большего горизонтального ускорения. Если же мы имеем дело с ошибкой по высоте, то можно получить еще более неудачные соотношения. Допустим, что одна рука совершает более высокий бросок, за которым следует несколько низкий, таким образом, что два мяча прилетают почти в одно и то же время. Если бросок должен быть сделан в половине нормального времени, то это потребует четырехкратного вертикального ускорения. При жонглировании 7ю мячами, подобная коррекция, вероятно, будет за пределами человеческих возможностей.
Я считаю, что в конечном итоге кто-то будет жонглировать 13 мячами, а выброс 15 не кажется таким уж маловероятным. Но как кто-то сможет научиться плавно жонглировать 13 мячами, не тратя много лет, пытаясь плохо жонглировать 13ю мячами? Это, вероятно, потребует новых методов обучения; например, техника, которая позволит жонглеру отрабатывать броски мячами на скорости жонглирования 15 мячами, не беспокоясь о том, чтобы ловить и собирать их каждые несколько секунд. Но это уже тема для отдельной статьи.
Дополнительные материалы от переводчика
Текущий количественный рекорд в жонглировании мячами принадлежит Алексу Бэррону (Alex Barron) - выброс 14 мячей.
Текущий рекорд 13ю мячами также принадлежит Алексу Бэррону - 15 кетчей
Максимальный "сайтсвопный" бросок равен "z" т.е. 35, и принадлежит Крису Ходжу (Chris Hodge) - z(31^16).
Аналогичное исследование с ориентированием на максимальное ускорение руки (с участием Алекса Бэррона) - "Why it's almost impossible juggle 15 balls". Подобное исследование с раздельными замерами максимальной высоты и максимальной частоты -
The One Show - juggling maximum.
Иногда устанавливаются новые рекорды. Актуальные мировые рекорды можно посмотреть на JuggleWiki.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Последние комментарии