Физика жонглирования

Bengt Magnusson и Bruce Tiemann

прим. переводчика — оригинал "The Physics of Juggling by Bengt Magnusson and Bruce Tiemann" можно найти здесь. Также обращаю внимание, что статья датируется 1989 годом, то есть с момента её написания прошло более 20 лет, и вполне естественно, что все события о которых говорится "в настоящее время", могли несколько устареть. Законы физики, впрочем, остаются прежними.

Жонглирование — искусство контролирования находящихся в воздухе объектов, число которых превышает количество рук, удивляло и восхищало людей на протяжении тысяч лет. Начиная с древних египетских иероглифов, старой японской резьбы по дереву и до современных фотографий, мы можем наблюдать историю манипулирования различными предметами. В записях 4000-летней давности есть упоминание о некоем египтянине, жонглировавшем девятью мячами. Также есть записи о двух японских жонглёрах, живших несколько сотен лет назад. Об одном утверждается, что он остановил войну жонглируя девятью мячами. Враги бежали в панике, полагая, что только могущественный волшебник мог выполнить подобный трюк. О другом говорится, что он мог жонглировать семью мечами. Ранее, в нашем (прим. переводчика — уже в позапрошлом) столетии, Jenny Yaeger и Enrico Rastelli установили рекорд, как единственные люди, продемонстрировавшие жонглирование десятью мячами. В дальнейшем это количество превзошли, хотя и с более простым жонглёрским реквизитом, Сергей Игнатов и Альберт Петровский, успешно показавшие жонглирование одиннадцатью кольцами. Впрочем, жонглёрам совсем не обязательно требуется огромное число предметов чтобы удивлять зрителей, что успешно демонстрируют современные артисты, такие как Michael Moshen и Airjazz trio. Жонглирование тремя мячами обладает достаточным потенциалом для поддерживания жонглёрского креатива на протяжении всей жизни.

Многие люди задаются вопросом: "Как жонглёрам удаётся выполнять все те трюки, которые они делают? Как возможно контролировать все объекты находящиеся в воздухе?". Первым шагом для ответа на этот вопрос станет выявление базовых физических законов, описывающих движение. Будучи и физиками, и активными жонглёрами, мы намеревались открыть некоторые из этих законов почти три года назад во время выпускного года в Калифорнийском технологическом институте. При том, что физические уравнения не выходят за рамки уровня первокурсника, решение задачи оказалось очень интересным, и давало возможность проверки "играя на берегу моря".

Основное наблюдение, общее для всех жонглёров, заключается в том, что всё базовое жонглирование исполняется в крайне строгих паттернах, где каждая рука делает точные одинаковые движения. Базовый паттерн жонглирования, который выполняется одинаково независимо от используемого реквизита, доступен в двух вариантах. Один используется при жонглировании нечётным числом предметов, другой же для чётного числа предметов. При нечётном числе предметов, каждая рука бросает предметы по параболе в другую руку, где они впоследствии ловятся и бросаются обратно по аналогичной траектории. Предметы отпускаются близко к центру паттерна, а ловятся на наружной стороне. Параболические траектории полётов пересекаются перед жонглёром, и каждый предмет посещает обе руки. Такой паттерн называется каскадом (Рис. 1.). Для чётного числа предметов, броски также бросаются изнутри, но ловятся той же самой рукой снаружи. Получаются две непересекающиеся траектории полётов, а предметы никогда не перелетают из руки в руку. Такой паттерн называется фонтаном (Рис. 2.). Для большинства не-жонглёров характерно неверное представление, будто всё жонглирование происходит по "круговому" паттерну. Такая вариация называется круг (Рис. 3) и определённо сложнее, чем паттерны описанные выше. В круге, существует только одна парабола вместо двух, в результате чего требуется или выделять намного меньше времени для каждого броска, или же делать броски на значительно бо́льшую высоту. В обоих случаях жонглирование значительно усложняется. Паттерн, представляющий из себя нечто среднее между каскадом и кругом, называется полукаскад, и также широко распространён.

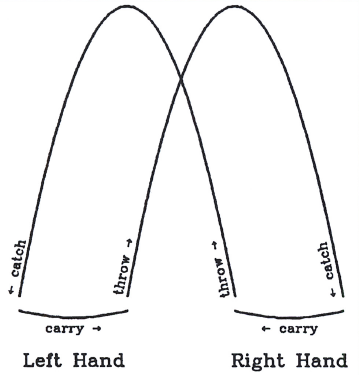
Рис.1. Паттерн каскад используется при жонглировании нечётным числом предметов

Рис.2. Паттерн фонтан используется при жонглировании чётным числом предметов

Рис.3. Круг имеет только одну параболу и намного сложнее в исполнении.

Чтобы определить соотношение между высотой бросков и числом мячей в базовых паттернах, введём несколько переменных. Давайте обозначим время между двумя последовательными бросками из одной руки как τ. Предмет некоторое время всегда удерживается в руке: это ловля, перенос в положение для броска и выпускание мяча. Обозначим это время как θτ. θ, в данном случае, это доля времени потраченная на удерживание мяча, и 0<θ<1. Число задействованных в жонглировании предметов обозначим как n, а высоту бросков как h.

Для начал предположим, что n — чётное. Каждая рука держит ½n предметов, и на полный цикл потребуется ½nτ секунд. В то же время, из-за наличия времени удерживания, первый предмет должен прилететь раньше на время θτ, и таким образом время t, которое каждый объект находится в воздухе составляет t=½nτ - θτ = ½τ(n - 2θ). Данная формула подходит и для нечётных чисел, хотя вывод будет несколько отличаться. Так как h = 1/8gt² мы получаем, что при t = ½τ(n - 2θ),

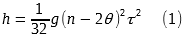
прим. переводчика — на всякий случай, если вдруг кого-то данные рассуждения приведут в замешательство, напомню, что τ — это время между бросками с одной руки. Если бы τ было временем между бросками с разных рук, то полное время цикла составило бы просто nτ секунд (но при этом τ было бы в два раза меньше).
И насчет формулы 1/8gt². Очевидно, что под t подразумевается время полета мяча (т.е. время в течении которого мяч летит вверх + время когда мяч летит вниз). Высота падения равняется h = ½gt², а поскольку время полета вниз равно времени полета вверх, то высота броска относительно общего времени полета будет равна h = ½g(t_полета/2)² = ½*(gt_полета²/4) = 1/8 gt²

n - 2θ будет средним по времени числом предметов, находящихся в воздухе. Для большинства жонглёров θ приблизительно равна 0,5. Причина по которой θ=0,5 заключается в очень строгом ритме: одна рука делает бросок точно в тот момент, когда другая рука ловит мяч. τ варьируется от 0,2 с до 0,8 секунд. В большинстве случаев τ ≈ 0,5 c.

τ и h являются ограничивающими факторами, определяющими жонглирование. h ограничивается точностью броска, т.к. высокие броски должны бросаться точнее чем низкие, а τ ограничивается тем насколько быстро можно жонглировать, сохраняя достаточную точность бросков. Легче сделать точный бросок, если выделить на него достаточно много времени, особенно если вы спешите. Для простоты полагаем, что предметы представляют собой точки. Благодаря этому допущению мы обходим стороной анализ столкновений между предметами, который представляет собой весьма сложную проблему для решения, особенно с большим вращающимся реквизитом, таким как булавы. Обозначим ширину каждой дуги как s, с долей ошибки Δs на каждой стороне. Обозначив начальную скорость брошенного предмета как ν₀, а угол отклонения от вертикали как α, с ошибкой Δα, которая в свою очередь может привести к увеличению ошибки по ширине Δs (Рис. 4). Чтобы достигнуть высоты h нам потребуется вертикальная скорость ν_0z = (2gh)^½. Тогда отношение горизонтальной скорости к вертикальной ν_0x/ν_0z = tg α, откуда получаем что ν_0x = ν_0z tg α и s = tν_0x=(8h/g)^½ν_0z tg α = 4h tg α, или α = arctg(s/4h). Теперь α + Δα = arctg[(s + Δs)/4h], откуда Δα = arctg[(s + Δs)/4h - arctg(s/4h). Поскольку arctg(x) = x + выражение порядка x³ и выше, получаем

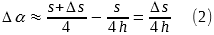
прим. переводчика — отмечу, что преобразование arctg(s/4h)≈s/4h допустимо только при маленьких значениях s/4h. Так для значений s=0,9 и Δs=0,3 погрешность в вычислении Δα составляет не более 5% при высоте броска от 1,2 метра, и не более 1% при высоте броска 2,65 м. А вот при высоте бросков в 0,5 метра, погрешность вычислений составит более 25%, и разумеется, игнорировать такие погрешности не стоит.

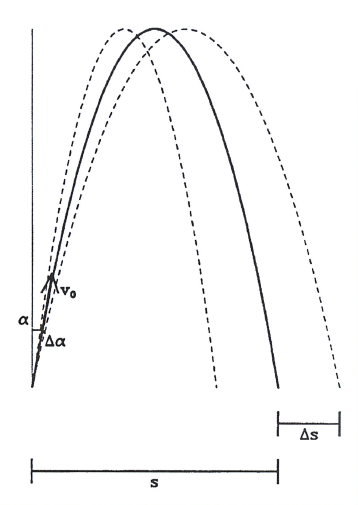
Рис. 4. Геометрическая ошибка при броске.

Δs составляет около 0,3 метра для большинства жонглёров, в том числе и для паттернов, исполняемых лучшими жонглерами на высоте около 6 метров, как, например, 11 колец Сергея Игнатова. Что даёт Δα = 0,6°! То есть Игнатову требовалось выбрасывать каждое кольцо с точностью около 0,6° чтобы быть в состоянии поймать их. Для того чтобы избежать столкновений может потребоваться даже большая точность. При α = arctg(s/4h)≈s/4h, мы может преобразовать Δα/α ≈ (Δs/4h)/(s/4h) = Δs/s, т.е., соотношение ошибки по углу не зависит от высоты броска и, при s в пределах 0,9 м, погрешность должна составлять около ⅓ для большинства жонглёров.

прим.переводчика — опять же, преобразование допустимо только при малых значениях s/4h. Оценка вполне правдоподобна при высоте броска от 2,25 м. А при высоте броска в 0,25 м отношение Δα/α=0,195 вместо 0,33.

Δα ограничивает высоту броска, а с учетом τ, получается число мячей котором можно было бы жонглировать. В принципе, за счет увеличения θ может уменьшить h, тем самым увеличив Δα, но при этом теряется ритм паттерна, а также уменьшается время за которое рука ловит следующий прилетающий предмет: τ(1 - θ). Для типичного жонглёра, с τ = 0,5 с и θ = 0,5, желающего жонглировать семью мячами, высота каждого броска должна быть, согласно выражению (1), около 2,8 метра. Если тот же жонглёр переместится на Луну, где g составляет 1/6 от этого же значения на Земле, при сохранении прежних значений τ, θ, и h, то мы можем решить уравнение относительно n и найти каким число мячей мы смогли бы жонглировать на Луне. n = 2θ + τ^-1(32h/g_moon)^½ ≈ 15,7 или 15 мячей. Пятнадцать — достаточно небольшое число, чтобы получилось расположить все мячи в паттерне без того, чтобы они постоянно сталкивались. Можно было бы утверждать, что само количество мячей в воздухе будет ошеломляюще сложным для мозга, чтобы суметь его обрабатывать, и таким образом жонглирование 15 мячами будут невозможным. Но наш опыт говорит, что это не так. Мозг учится распознавать образы для больши́х чисел за удивительно короткий период времени, гораздо быстрее, чем развиваются необходимые двигательные навыки. Даже проблема удержания 15 мячей в двух руках в начале жонглирования, с последующим выбрасыванием по контролируемой схеме не является непреодолимой. При необходимости можно использовать жонглирующую машину для запуска паттерна. Поэтому мы считаем, что 15 мячей — это вполне разумное количество, которым можно жонглировать на Луне. На текущий момент лучшие земные жонглёры могут контролировать до 9 мячей одновременно; на Луне они должны были бы суметь удерживать в воздухе около 19 мячей!

При жонглировании n объектами, можно задаться вопросом, какова высота на которой можно жонглировать другим числом предметов m, при сохранении τ и θ константами. Как правило, большинство людей отвечают, что удвоение числа предметов требует увеличения высоты паттерна в четыре раза, но они забывают об эффекте θ. Правильный ответ, выводимый из выражения.(1),

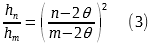
При θ = 0,5 мы получаем, например, что f₆/f₃ = 6,25, что заметно отличается от четырёх. Впрочем, как показывает практика, большинство жонглёров вместо того, чтобы в связи с увеличением h уменьшить Δα, предпочитают уменьшить τ, в результате чего h увеличивается несколько меньше чем этого можно было бы ожидать.

В процессе перекидывания предметов можно заметить, что броски на разные высоты могут быть скомбинированы в конкретные паттерны жонглирования, описываемые несколькими простыми правилами. Такие комбинации приводят нас к целому классу трюков в жонглировании, которые называются "сайтсвопы"( англ. "site swap" — смена места). Для начала мы сделаем небольшое введение в нотацию, придуманную Полом Климаком (Paul Klymack) из Санта Круз (Santa Cruz), который независимо от от нас обнаружил класс таких трюков. В данной нотации, цифра n обозначает путь по которому надо бросить мяч если мы собираемся жонглировать соответствующим числом предметов. Так, 3 означает, что мяч бросается по низкой дуге из руки в руку, 4 — немного более высокий бросок, но направленный в ту же руку, 5 намного более высокий бросок из руки в руку и т.д. 0 обозначает пустую руку, 1 быстрый переброс из руки в руку, а 2 означает всего лишь удерживание мяча в руке на протяжении одного такта. Если вы сейчас расположите цифры на одной линии, например 7 5 6 2, то такая последовательность иногда будет возможным паттерном для жонглирования без постоянных столкновений. Руки всё время выполняют требуемые действия через равные промежутки времени и бросают мячи согласно строке цифр. Мячи могут выкидываться на довольно широком диапазон высот, и паттерны иногда будут выглядеть довольно странно, но если всё сделать правильно, то предметы всегда, как будто по волшебству, будут прилетать обратно точно тогда, когда они будут нужны, и прямо туда, где они будут нужны.

Каковы же критерии правильной строки цифр? Перво-наперво, среднее арифметическое от всех цифр должно быть равно числу мячей которым собираешься жонглировать. Например, для 7 5 6 2 среднее арифметическое равно 5, следовательно, это должен быть трюк с пятью мячами. Но это еще не всё. Также надо убедиться, что два мяча никогда не прилетят в одну руку в одно и то же время. Опять же возьмём 7 5 6 2. Так как это трюк с пятью мячами, мы можем нормализовать числа на пять, и получим 2 0 1 -3. (Среднее арифметическое таким образом стало равно нулю.) 2 свидетельствует о том, что мяч, брошенный в этой позиции, прилетает двумя позициями позднее, на позицию три. Мяч на позиции три перемещается вперед на одну позицию, то есть на четвертую. Мяч на позиции четыре перемещается на три позиции назад, на позицию один. (Мяч на первой позиции всегда приходит с противоположного направления). Наконец, мяч на позиции два остается на ней же. Таким образом получается, что, после одного полного цикла, нет двух мячей которые бы занимали одну позицию. (прим. переводчика — к сожалению авторы не написали что делать, если необходимая позиция для перемещения вперёд/назад отсутствует, как, например, для вполне возможных сайтсвопов 51, 723, 714 и т.п. В таком случае позиции продолжают отсчитываться с начала/конца паттерна. Подробнее можно почитать здесь) Приведём пример невозможного трюка, такого как 8 5 4 3. В данном случае среднее арифметическое также равно пяти и строка преобразовывается в 3 0 -1 -2. В данном случае 0, -1, и -2 приходят на вторую позицию, что приводит к тройному столкновению. Лучший способ обнаружения возможных трюков — сгенерировать их на компьютере. Сделав это, мы сгенерировали несколько тысяч трюков, 99,9 процентов из которых были полностью неизвестны другим жонглёрам ранее. Если вы жонглёр, и хотите удивить своих друзей-жонглёров, попробуйте некоторые из этих трюков: 4 4 1 и 5 1 4 1 4 с тремя мячами, 7 5 3 1 и 8 5 2 4 2 с четырьмя, и 6 6 6 6 1, 7 5 6 2, 7 5 7 5 1, и 9 5 5 5 1 с пятью мячами. С точки зрения математики интересно знать, что набор всех сайтсвопов длиной n (вместе с операциями композиции функций) формируют группу изоморфную к Sym(n).

прим. переводчика — с последним предложением сложная ситуация. С одной стороны, я не разбираюсь в теории групп от слова "совсем". С другой стороны, я точно знаю, что если нет ограничения по максимальному числу мячей (или по максимальному броску), то число возможных сайтсвопов будет бесконечным в независимости от их длины. Если же принять за b максимальное число мячей, то число сайтсвопов длиной n будет составлять (b+1)ⁿ, а sym(n) это что-то вроде n! (если я правильно понял). В общем, авторы либо излишне перемудрили, либо я дурак и ничего не понял. Во втором случае — отпишитесь в комментариях, объясните как там на самом деле :)

Полученные результаты применимы ко всему существующему реквизиту: мячи, кольца, и булавы. Булавы требуют введения новых переменных для анализа. Они вращаются в полете, и должны быть пойманы за ручку. (Кольца тоже вращаются в полете, но для их ловли фактор вращения значения не имеет). Данное условие, вкупе с их значительным размером, делает булавы вероятно наиболее сложным реквизитом для жонглирования, и официальный мировой рекорд составляет только семь булав (прим. переводчика — уже 9). Анализ вращения булавы дал несколько неожиданный результат. При более высоком броске булавы, она будет вращаться в воздухе более длительное время, что приводит к тому, что при естественном двойной обороте булава должна быть брошена в четыре раза выше, чем на один оборот. Данное обстоятельство приводит к тому, что когда мы бросаем булавы выше, их также приходиться дополнительно подкручивать, и двойной оборот в точности соответствует удвоенной высоте одиночного оборота.

Рассмотрим следующую модель броска булавы. Булава бросается поворотом предплечья руки относительно фиксированной точки (локтя), с расстоянием l от локтя до центра масс булавы (Рис. 5). Обозначим за l₁ расстояние от локтя до конца ручки булавы. Если при броске жонглёр задействует движение запястьем (варьируется от жонглёра к жонглёру), то l может отличаться от расстояния от локтя до центра масс булавы, но всё равно будет существовать некоторый эффективный рычаг руки leƒƒ, который будет оставаться относительно неизменным для любого жонглёра. То же самое справедливо и дляl₁. Обозначим угловую скорость предплечья как ω. Тогда центр масс булавы выбрасывается со скоростью ν₀ = ωl, и остаётся в воздухе на время t = 2ν₀/g = 2ωl/g с. Конец ручки стартует со скоростью ν₁=ω(l - l₁). Относительно центра масс, конец ручки будет иметь скорость ν₀ - ν₁ = ωl - ω(l - l₁), остающейся неизменной на протяжении всего броска. Очевидно, что ручка вращается с той же угловой скоростью ω, что и предплечье.

прим. переводчика — мне почему-то не было очевидно, каким образом скорость вращения булавы совпадает со скоростью вращения предплечья. То ли авторы что-то напутали, то ли у меня проблемы с техническим английским. В общем, вывод авторов (хотя и верный) мне не показался интуитивно понятным и вызвал больше вопросов, чем ответов. Поэтому на всякий случай приведу собственный вывод угловой скорости вращения булавы.
Центр масс булавы действительно выбрасывается со скоростью ν₀ = ωl. Но конец ручки покидает руку со скоростью ν₁=ω l₁. Вот теперь все логично — скорость вылета равна угловой скорости предплечья на длину рычага.
Тогда скорость движения конца ручки относительно центра масс будет ν₀ - ν₁ = ωl - ωl₁ = ω(l - l₁)
а угловая скорость вращения булавы (т.е. ручки относительно центра масс) ω_булавы будет равна линейной скорости конца ручки ν₀ - ν₁ поделенной на радиус вращения, равный (l - l₁). Т.е. ω_булавы = (ν₀ - ν₁)/(l - l₁) = ω(l - l₁)/(l - l₁) = ω

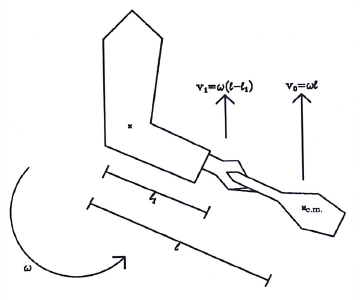
Рис. 5. Кинематика броска булавы.

При этом за m оборотов булава повернётся на угол 2πm за время t_m = 2πm/ω. Это время должно равняться ранее вычисленному времени: 2πm/ω = 2ωl/g, или ω = (mπg/l)^½. А высота броска будет равна

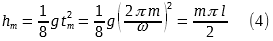
Отметим, что h_m является линейной функцией от m. Другим важным следствием из этой формулы является её независимость от g. Причина заключается в том, что чем меньше g, тем выбрасывание булав делается медленнее, в сравнении с броском на на ту же высоту с большим g. В таком случае автоматически уменьшается скорость вращения булавы, но поскольку g меньше, булава дольше остается в воздухе, что компенсирует медленное вращение.

Если вы когда-либо видели хороших жонглёров пятью булавами, попробуйте при подходящем случае моргать глазами как можно быстрее, пока смотрите на паттерн. При этом можно заметить, что все булавы располагаются параллельно. Такое происходит только при жонглировании нечётным числом булав. Чётное количество булав будет иметь другие, менее характерные конфигурации. Почему так происходит? Примем, что n = число булав, m = число оборотов, а ω, τ, и θ остаются прежними. В то время как каждая рука делает бросок каждые τ секунд, время между последующими бросками с правой и левой рук составляет ½τ. Расхождение по углу между двумя выброшенными булавами составляет β = ½ω τ. С h_m = mπl/2 = 1/32g(n - 2θ)²τ² мы получаем l = g(n - 2θ)²τ²/16mπ, и ω = (mπg/l)^½ = 4mπ/(n - 2θ)τ, откуда

Как можно заметить, при параллельных булавах β = 180°, что будет верным только при n = 2(m + θ). n должно быть целым, и таким образом θ должно быть равно 0, 0,5, или 1. Поскольку θ = 0 или 1 физически невозможно, остается только θ = 0,5 и n = 2m + 1. Так как у большинства жонглёров θ довольно близко к 0,5, при том, что три булавы кидаются на один оборот, пять на два, а семь на три и т.д., то параллельное расположение булав встречается довольно часто. Булавы могут располагаться параллельно и при β = 360°, как, например, для пяти булав бросаемых на четыре оборота, но подобное исполнение встречается значительно реже. Для θ = 0,5, также существуют следующие интересные углы: 90° для пяти булав на один оборот; 120° для четырех на один и для семи на четыре оборота; 270° для пяти на три оборота. Нам удалось заснять большинство этих ракурсов на фотографиях, что добавило нам уверенности относительно рассмотренной простой модели жонглирования булавами. На фотографии ниже авторы жонглируют четырьмя и пятью булавами на два оборота, демонстрируя β = 240° и β = 180° соответственно (рис. 6).

Рис. 6. Авторы жонглируют четырьмя и пятью булавами

Мы выражаем благодарность всем нашим друзьям-жонглёрам, которые аккуратно выступили перед камерами и останавливались, чтобы помочь в согласовании наших теорий. В особенности хотелось бы отметить Dan Bennett, David Deeble, Barry Friedman, Daniel Holzman, Tyler Linkin, Bob Mendelson, и Owen Morse. Мы смогли увидеть, как паттерны жонглирования подчиняются чудесно простым физическим законам. В настоящее время уже никто не разбегается в ужасе при виде умелых жонглёров, но хотя физическая основа жонглирования и определена, биологические вопросы, касающиеся того, как именно жонглёры применяют эти правила и согласовывают моторные навыки остаются открытыми.

Bengt Magnusson получил степень бакалавра физики в Калифорнийском технологическом институте в 1987 году и в настоящее время является аспирантом третьего курса Калифорнийского университета в Санта-Барбаре. Область его исследований — экспериментальная астрофизика частиц. Он жонглирует чуть более трех лет и достиг уровня девяти мячей/пяти булав.

Bruce Tiemann получил степень бакалавра по химии в Калифорнийском технологическом институте в 1987 году и в настоящее время работает с нелинейными оптическими соединениями в Лаборатории реактивного движения в Пасадене. Он жонглирует около десяти лет и "достаточно хорошо" выступает с семью булавами и восемью мячами. Среди других увлечений: создание лазеров и любительское радио.