Физика жонглирования мячами
Цель этой статьи — попробовать объяснить некоторые физические основы жонглирования мячами. В отличие от математической теории жонглирования, где количество рук и продолжительность бросков не имеют значения, в этой статье данные величины играют центральную роль.
Текущий вариант текста находится в состоянии разработки и, как мы надеемся, будет впоследствии дополнен.


Время бросков
Мы будем рассматривать реальный паттерн жонглирования, чтобы увидеть, что именно происходит. Получим информацию о тайминге паттерна, выведем первую теорему Шеннона о жонглировании и закончим исследованием как быстро/медленно можно жонглировать не меняя высоту бросков.
Чтобы провести анализ мы сделали ряд снимков реального выполнения сайствопа 4444535344. Снимки были сделаны с частотой 30 кадров в секунду. Один из снимков представлен выше. прим. переводчика - там же, для удобства, я добавил гифку, сделанную из всех остальных снимков. В таблице 1 приведен тайминг происходящих событий.
| время | рука | мяч | такт | событие |
|---|---|---|---|---|
| 0,100 | П | зеленый | 1 | бросок 4 |
| 0,267 | Л | желтый | 2 | бросок 4 |
| 0,433 | Л | красный | кетч | |
| 0,467 | П | синий | 3 | бросок 4 |
| 0,633 | П | зеленый | кетч | |
| 0,700 | Л | красный | 4 | бросок 4 |
| 0,867 | Л | желтый | кетч | |
| 0,933 | П | зеленый | 5 | бросок 5 |
| 1,100 | П | синий | кетч | |
| 1,167 | Л | желтый | 6 | бросок 3 |
| 1,367 | Л | красный | кетч | |
| 1,467 | П | синий | 7 | бросок 5 |
| 1,600 | Л | красный | 8 | бросок 3 |
| 1,633 | П | желтый | кетч | |
| 1,800 | Л | зеленый | кетч | |
| 1,967 | П | желтый | 9 | бросок 4 |
| 2,067 | Л | зеленый | 10 | бросок 4 |
| 2,100 | Л | красный | кетч |
Таблица 1. В таблице приведены все события, происходящие на фотографиях, с привязкой ко времени. Т.о., у нас есть время и порядок всех бросков и кетчей.
Частота бросков
Наша первая цель — измерить частоту бросков. Применив к данными из таблицы метод наименьших квадратов, мы получили следующее линейное выражение t(n) = 0,229·n - 0,187, где t(n) обозначает время броска n. Это показано на рисунке 1. Как можно увидеть, один такт длится примерно 229 мс, но во второй половине правая рука начинает немного отставать.
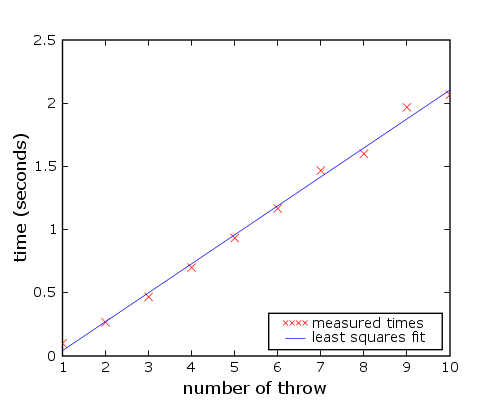
Рисунок 1. Применив метод наименьших квадратов ко времени бросков, мы получили выражение t(n)=0,229·n-0,187. Т.о., продолжительность одного такта составляет приблизительно 0,229 секунды.
Время удерживания
Между бросками, перед тем как поймать мяч, руки некоторую часть времени перемещаются пустыми. Другая часть времени тратится на удерживание или переноску мячей. Это показано на следующем рисунке.
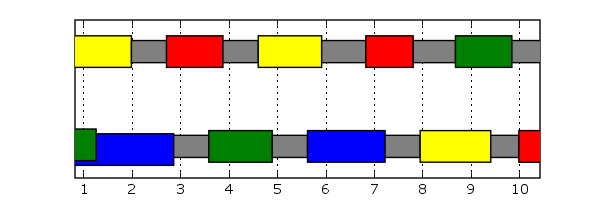
Рисунок 2. Графическая иллюстрация времени удерживания: верхняя полоса соответствует левой руке, нижняя полоса — правой. Серые полоски означают, что соответствующая рука пустует. Единицы измерения на горизонтальной оси — такты.
В самом начале рассматриваемой последовательности бросков правая рука держит 2 мяча (зеленый и синий). По некоторым понятным соображениям в дальнейших расчетах данная начальная фаза не рассматривается. Все расчеты начинаются с момента выброса зеленого мяча после которого в каждой руке находится не более одного мяча.
- В любой момент времени каждый мяч находится либо в состоянии полета, либо удерживается в руке. Т.о., для каждого интервала времени справедливо следующее равенство
сумма времен полета + сумма времен удерживания =
= количество мячей·длина интервала - В любой момент времени каждая рука либо держит мяч, либо нет (пустует). Т.о., для каждого интервала времени также справедливо и следующее выражение
сумма времен удерживания + сумма времен ожидания =
= количество рук·длина интервала
Объединив эти выражения, получаем
| сумма времен удерживания + сумма времен ожидания | = | сумма времен полета + сумма времен удерживания |
| количество рук | количество мячей |
Т.о. мы пришли к результату, впервые обнаруженному известным математиком Клодом Шенноном (Claude Shannon).
Теорема 1 (Первая теорема Шеннона). Для (не обязательно периодического) жонглирования, при условии, что каждая рука держит не более одного мяча за раз, для каждого интервала времени справедливо следующее выражение:
| сумма времен удерживания + сумма времен полета | = | количество мячей |
| сумма времен удерживания + сумма времен ожидания | количество рук |
Для большей наглядности, проверим справедливость теоремы для нашего частного случая последовательности бросков.
| левая | правая | ||
|---|---|---|---|
| удерживание (holding) | ожидание (empty) | удерживание (holding) | ожидание (empty) |
| 1,234 | 0,766 | 1,368 | 0,632 |
| 0,100-0,267 | 0,100-0,467 | ||
| 0,267-0,433 | 0,467-0,633 | ||
| 0,433-0,700 | 0,633-0,933 | ||
| 0,700-0,867 | 0,933-1,100 | ||
| 0,867-1,167 | 1,100-1,467 | ||
| 1,167-1,367 | 1,467-1,633 | ||
| 1,367-1,600 | 1,633-1,967 | ||
| 1,600-1,800 | 1,967-2,100 | ||
| 1,800-2,067 | |||
| 2,067-2,100 | |||
Таблица 2. Измерение времен удерживания и ожидания мячей на интервале времени с t=0,100 по t=2,100.
| зеленый | желтый | синий | красный | ||||
|---|---|---|---|---|---|---|---|
| воздух | рука | воздух | рука | воздух | рука | воздух | рука |
| 1,433 | 0,567 | 1,199 | 0,801 | 1,266 | 0,734 | 1,500 | 0,500 |
| 0,100-0,633 | 0,100-0,267 | 0,100-0,467 | 0,100-0,433 | ||||
| 0,633-0,933 | 0,267-0,867 | 0,467-1,100 | 0,433-0,700 | ||||
| 0,933-1,800 | 0,867-1,167 | 1,100-1,467 | 0,700-1,367 | ||||
| 1,800-2,067 | 1,167-1,633 | 1,467-2,100 | 1,367-1,600 | ||||
| 2,067-2,100 | 1,633-1,967 | 1,600-2,100 | |||||
| 1,967-2,100 | |||||||
Таблица 3. Измерение времен удерживания в руке и полета мячей на интервале времени с t=0,100 по t=2,100.
Пример. Для описанной выше последовательности, в рассматриваемом двухсекундном интервале времени, начинающегося с t=0,100, мы берем времена удерживания и ожидания, указанные в таблице 2. Времена для мячей приведены в таблице 3. Как можно заметить, левая рука пустует в течении 38.3% от всего времени (0,766с из 2с интервала), а правая рука пустует в течение 31,6% от всего времени (0,632с из 2с). Переменные используемые в первой теореме Шеннона будут равны
| сумма времен удерживания | |
| = 1,234 + 1,368 = 0,567 + 0,801 + 0,734 + 0,500 = 2,602 | |
| сумма времен ожидания | |
| = 0,766 + 0,632 = 1,398 | |
| сумма времен полета | |
| = 1,433 + 1,199 + 1,266 + 1,500 = 5,398 | |
Т.о. для левой части уравнения Шеннона получаем (2,602+5,398)/(2,602+1,398) = 8/4 = 2, как и ожидалось.
Стандартные паттерны
Как сказано выше, для теоремы Шеннона не обязательно, чтобы паттерн жонглирования был периодическим. Но, если применить теорему к таким паттернам как 3 или 4, где все броски имеют одинаковую высоту, то её можно значительно упростить.
Определение. Паттерн жонглирования называется стандартным, если каждый мяч каждый раз когда он ловится удерживается одинаковое время. Каждый мяч при каждом броске летит на протяжении одного и того же времени. Между каждыми двумя последовательными бросками руки пустуют в течение одинакового времени, и каждая рука в любой момент времени держит не более одного мяча.
Теорема 2 (первая теорема Шеннона для стандартных паттернов). Для стандартных паттернов жонглирования справедливо следующее соотношение:
| время удерживания + время полета | = | количество мячей |
| время удерживания + время ожидания | количество рук |
Доказательство. Сведем данное утверждение к общей версии теоремы Шеннона. Обозначим время удерживания как h (holding time), время полета как f (flight time), время ожидания как e (empty time), число мячей как b. Рассмотрим любой временной интервал продолжительностью h+f. В течение этого интервала каждый из мячей летит f единиц времени, и т.о., сумма времен полета равняется f·b (см. рис. 3). Кроме этого, в течение данного интервала времени каждый мяч удерживается h единиц времени, и т.о., сумма времен удерживания составляет b·h. В итоге, каждый мяч бросается ровно один раз за временной интервал, и т.о., сумма времен ожидания равна b·e. Применив теорему 1, получаем
| количество мячей | = | b·h + b·f | = | h+f |
| количество рук | b·h + b·e | h+e |
Что и требовалось доказать.
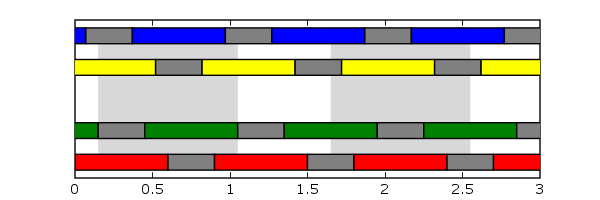
Рисунок 3. Временная диаграмма для стандартного жонглирования 4-мя мячами 2-мя руками. Одна рука жонглирует синим и желтым мячами, а другая красным и зеленым. По горизонтальной оси отмечается время. Время удерживания отмечено серым цветом, время полета — в цвет мяча. Время удерживания h=0,3, время полета f=0,6. Светло-серые участки на заднем плане обозначают два различных временных интервала длиной h+f. Из диаграммы видно, что каждый временной интервал данной длины содержит равное количество сумм времен удерживания, полета и ожидания.
Скорость жонглирования
Хорошие жонглеры могут в некоторой степени варьировать скорость паттерна сохраняя при этом высоту бросков. Крайние случаи называются "жонглирование горячей картошкой"/"hot potato juggling" (мячи бросаются незамедлительно, сразу после того как будут пойманы) и "ленивое жонглирование"/"lazy juggling" (мяч удерживается в руке так долго, как только возможно). Поскольку высота броска определяется временем полета (выражение будет рассмотрено ниже), сохранение высоты бросков означает, что время полета не изменяется. Так насколько же быстро или медленно мы можем жонглировать, сохраняя заданное время полета f?
Теорема 3 (скорость жонглирования с фиксированным временем полета). Для стандартных паттернов жонглирования h руками с равномерно распределенными бросками, при количестве мячей b>h и с временем полета f, длина такта может варьироваться от f/b до f/(b-h).
Доказательство. В предельном случае "жонглирования горячей картошкой" время удерживания равно 0. Подставив данное значение в теорему 2, получаем
| время ожидания = | f·h |
| b |
Поскольку время удерживания равно нулю, то время между бросками с одной руки будет равно f·h/(b+0)=f·h/b. Предполагая, что броски равномерно распределены по всем h рукам, получаем, что длина такта при "жонглировании горячей картошкой" со временем полета f будет равна f/b.
В предельным случае “ленивого жонглирования” время ожидания равно нулю. Из теоремы 2 получаем
| время удерживания = | f·h |
| b-h |
и, поскольку время ожидания равно нулю, длина такта для "ленивого жонглирования" с временем полета f будет равна f/(b-h). Что и требовалось доказать.
Пример. Для рассмотренного жонглирования из таблицы 1 среднее время полета составляет приблизительно 0,6 с. Поскольку в паттерне участвуют 4 мяча и две руки, длина такта для стандартного паттерна может находится между 0,6/4=0,15 секунды и 0,6/(4-2)=0,30 секунды. Продолжительность тактов, которую мы замерили для (неоднородного) паттерна в таблице 1, составила 0,229 секунды (см. рис.1), что находится почти точно в середине указанного интервала.
Геометрия бросков
В течение всего времени полета на движение мяча влияет только сила земного притяжения (сопротивлением воздуха можно пренебречь). Поэтому горизонтальная составляющая скорости мяча остается постоянной на протяжении всего полета, в то время как вертикальная составляющая испытывает ускорение g=9,81м/с2 направленное вниз. Решив уравнение движения, мы получаем, что, учитывая начальное положение x(0) и начальную скорость v(0), мяч следует по параболе (сравните с рисунком 4):
горизонталь: x1(t) = x1(0) + v1(0)t
вертикаль: x2(t) = x2(0) + v2(0)t - 0,5gt2

Рисунок 4. Jochen Voss жонглирует тремя светящимися мячами. Выделенный мяч движется слева направо по зеленой параболе. Мячу требуется 0,567с чтобы преодолеть обозначенный участок пути, сначала поднимаясь на 45,9 см, а затем опускаясь на 33,4 см.
Ссылки
- Burkhard Polster
The Mathematics of Juggling
Springer, New York, 2002
ISBN: 0387955135 - the Kinetic Books' Motion in Two Dimensions lab
Небольшой нюанс (от переводчика)
На всякий пожарный отмечу, что на сайте автора в конце статьи есть приписка:
Copyright © 2012, Jochen Voss. All content on this website (including text, pictures, and any other original works), unless otherwise noted, is licensed under a Creative Commons Attribution-Share Alike 3.0 License.
В чем суть. Если я правильно понимаю, то задействовать контент с сайта-источника можно, но при условии, что будет отдельно указано авторство произведения.
https://www.seehuhn.de/pages/physics.html - ссылка на источник. Автор: Jochen Voss.
А также, что производные от авторского произведения будут распространяться по этой же лицензии. Лично мне без разницы как будет использован перевод в дальнейшем и будут ли на него ссылаться (ну а вдруг?!), но вот ссылку на Йохана Восса лучше все же добавить. Всех благ!
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Последние комментарии