Оптимальное жонглирование
Анализ и переосмысление паттернов жонглирования
Перевод статьи Jack'а Kalvan'а Optimal Juggling
Введение
Жонглирование — одно из самых больших удовольствий в моей жизни, с тех пор как в 1980 году я научился жонглировать тремя мячами. Получив степень бакалавра в области машиностроения в Carnegie Mellon University, мне удалось объединить свои интересы в жонглировании и инженерии, работая в IBM Research над жонглирующим роботом. Хотя с тех пор я стал профессиональным артистом, я не переставал интересоваться техникой и математикой в своё свободное время. Данная статья является результатом моих исследований.
Математика жонглирования, вероятно, является даже более легкомысленным полем исследования, чем собственно само жонглирование. Тем не менее, мне удалось найти весьма интересные результаты, касательно того как должны выглядеть идеальные или пространственно оптимальные паттерны. Я верю, что полученные результаты могут помочь жонглёрам улучшить свои паттерны.
Говоря о пространственно оптимальных паттернах, я имею в виду схему жонглирования, при которой допускается одинаковое число ошибок во всех точках траектории полета, где столкновения наиболее вероятны. В основе лежит принцип, что сила цепи определяется силой самого слабого звена. Если жонглёр использует неэффективный паттерн с существенно большей вероятностью ошибки в одной области, чем в другой, то он будет тратить больше времени и сил.
Хотя жонглёры, как известно, бросают довольно разнообразный реквизит, включая булавы, кольца, котят и бензопилы, в этой статье будут рассматриваться только мячи, как и более распространенный реквизит, так и более простой для проведения анализа. Также, говоря об идеальных паттернах, будут рассмотрены только двумерные и не имеющие ошибок.
Паттерны в жонглировании состоят из двух частей: перемещение мячей и перемещение рук. В первую очередь я буду рассматривать жонглирование, касающееся перемещения мячей. Движения рук должны соответствовать позициям и скоростям мячей при бросках и ловлях, но я не буду проводить анализ этого движения, поскольку точное моделирование динамики человеческой руки не представляется возможным.
Я считаю, что руки должны соответствовать жонглированию, так же как руки эксперта-машиниста соответствуют раскладке клавиатуры. Жонглёры могут иметь собственные предпочтения относительно скорости и высоты жонглирования, в то время как другие параметры, такие как дальность броска и дальность перемещения руки могут быть оптимизированы.
Я также считаю, что в процессе тренировки, паттерны жонглёра развиваются методом проб и ошибок, постепенно приближаясь к пространственно оптимизированным паттернам. Как и в естественном отборе, плохие паттерны быстро умирают, в то время как хорошие паттерны живут долго и закрепляются. Я заметил, что после многих часов проб и ошибок, у лучших жонглёров наблюдаются пространственно оптимизированные паттерны. Мне кажется, что жонглёры могли бы ускорить свой процесс обучения, и улучшить свои навыки, предварительно взглянув на оптимальные паттерны до начала тренировки.
Я разработал компьютерную программу под названием Optimal Juggler (только для Macintosh), которая отображает оптимальные паттерны, описанные в этой статье. Пользователю предоставляется возможность отрегулировать множество факторов под свои предпочтения, после чего оптимальные паттерны будут незамедлительно вычислены и отображены на экране в реальном времени. Я настоятельно рекомендую сохранить у себя копию этой программы. В настоящий момент программа доступна для свободного скачивания через Интернет на сайте http://www.juggling.org/.
Физика жонглирования
Я введу несколько уравнений, касающихся тайминга жонглирования. Перво-наперво, мне требуется определить некоторые параметры. Во всех паттернах жонглирования мячи следуют по параболическим дугам. Термин дуга, используемый в статье, означает траекторию полета мяча, от броска до ловли. Также обозначим некоторые универсальные параметры жонглирования:
b = число мячей
h = число рук
f = время полета (время нахождения мяча в воздухе, от броска до ловли)
g = ускорение свободного падения (~ 9,81 м/с2)
Vh = горизонтальная скорость броска
Vv = начальная вертикальная скорость броска
H = высота броска
F = расстояние перелета (горизонтальное перемещение мяча в полете)
Клод Шеннон (Claude Shennon), хорошо известный по своему вкладу в областях математики и компьютерных наук, также провёл и первые исследования в области математики жонглирования. В своей работе он определил два параметра, которые я не упомянул ранее
d = время удерживания (dwell time) мяча в руке между ловлей и следующим броском
e = время ожидания (empty time) мяча в руке между броском и последующей ловлей
Теорема жонглирования Шеннона элегантно связывает между собой переменные, касающиеся времени жонглирования, с количеством жонглируемых объектов и числом рук.
b/h = (d+f)/(d+e)
Вместо того чтобы ссылаться в своей работе на переменные d и e, я решил, что неплохо бы включить эти величины в некоторые новые переменные:
τ = период руки или время между двумя бросками из одной руки. Вычисляется как d + e.
r = "коэффициент задержки" или доля времени, в течении которого рука держит мяч. Вычисляется как d/τ, или d/(d+e).
Ω = среднее количество находящихся в воздухе мячей, приходящихся на одну дугу. Вычисляется как f/τ, или f/(d+e).
Уравнения для переменной Ω можно переписать в виде
τ = f/Ω , или f=τ*Ω.
Нетрудно заметить, что коэффициент задержки, r, всегда находится между 0 и 1, и может быть описан как среднее количество мячей, занимающих руку во время жонглирования.
Подставляя новые переменные в уравнение Шеннона получаем:
b / h = Ω + r , или Ω = (b / h) - r.
Это важное уравнение, которое будет использовано в дальнейшем.
Разглядывая жонглёра, Ω можно найти, посмотрев на мячи в воздухе. Но, если при этом не смотреть на руки, может оказаться невозможным точно определить, сколько мячей участвует в жонглировании. Например, если мы видим жонглёра с двумя дугами мячей в воздухе и Ω = 1,25, нельзя сказать, жонглирует он тремя или четырьмя мячами. Чтобы определить это, потребуется оценить коэффициент задержки рук жонглёра, который может варьироваться от нуля до двух мячей.
По определению, для жонглирования требуется, как минимум, на один мяч больше, чем рук. Так, для 2 рук, Ω имеет минимальное значение 0,5, при b = 3 и r = 1.
В ньютоновской физике существуют уравнения, которые можно применить к брошенным объектам:
Vh = F/f
Vv = sqrt(2*g*H)
H = Vv2/(2*g),
Принимая, что броски и ловли происходят на одной и той же высоте, мы можем вывести уравнения для времени полета f и подставить его в другие уравнения. В результате получаем несколько полезных уравнений:
f = sqrt(8*H/g)
Vv = g * f / 2
H = g*f2/2 = g*[(τ*Ω)2]/8
Из этих выражений следует, что для двукратного увеличения времени полета, требуется удвоить начальную скорость броска, что в свою очередь означает четырехкратное увеличение высоты броска.
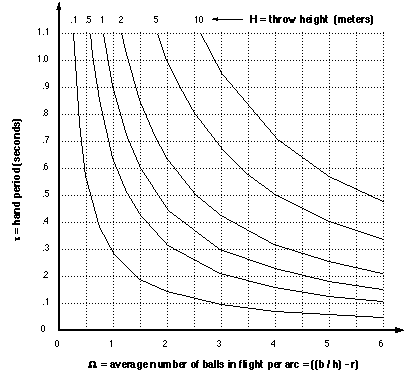
График 1: Зависимость высоты броска от τ и Ω
(принимаем, что бросок и ловля происходят на одной высоте, g = 9,81 м/с2)
Для следующих уравнений, мне понадобиться ввести переменные, обозначающие ошибки броска по позиции: dx, dy, и dz, ошибки броска по скорости: dvx, dvy, и dvz, и ошибки броска по времени dt. Рассмотрим, как различные ошибки броска влияют на полет мяча, сравнивая позиции мяча, брошенного правильно, с мячом, брошенным с каждой из возможных ошибок.
Ошибка в положении мяча во времени = t после броска
| ошибки по X | ошибки по Y | ошибки по Z | |
| Ошибка броска по позиции | dx | dy | dz |
| Ошибка броска по скорости | dvx*t | dvy*t | dvz*t |
| Ошибка броска по времени | dt*Vh | dt*[Vv-(g*t) + (dt*g/2)] | 0 |
| Общая ошибка на момент времени = t | dx + (dvx*t) + (dt*Vh) | dy + (dvy*t) + {dt*[Vv - (g*t) + (dt*g/2)]} | dz + (dvz*t) |
Глядя на эти уравнения, может показаться, что ошибки в положении мяча могут быть уменьшены за счет уменьшения времени полета, скорости броска, а также высоты и ширины дуг. На практике, уменьшение высоты паттерна действительно может уменьшить ошибку и сделать паттерн более стабильным. К сожалению, это также уменьшает время на совершение броска, что может усложнить выполнение точных бросков.
С другой стороны, ошибки можно уменьшить, ослабив временные ограничения для рук. Предоставление большего времени для каждого броска часто способствует увеличению точности бросков, даже если для это приходится увеличить высоту паттерна. Жонглёры должны найти компромисс между увеличением времени и увеличением точности, чтобы прийти к наиболее удобным и стабильным паттернам.
Обычно жонглёрам удобно расположить руки перед плечами (и немного ниже). Поскольку эта позиция находится примерно посередине диапазона досягаемости рук, она также обеспечивает бо́льшие возможности для ловли неточных бросков. Поэтому мы предполагаем, что расстояние между дугами в фонтане и расстояние перелета в каскаде будут эквивалентны ширине плеч жонглёра. Данные, полученные с записи жонглёров на видео, подтверждают эту гипотезу.
Настройка ошибок может быть очень сложной. Ошибки имеет тенденцию накапливаться. Например, после ловли мяча с большой ошибкой по положению, следующий бросок, скорее всего, будет хуже, чем в случае если бы ловля была хорошей. Умелый жонглёр способен поддерживать стабильный паттерн, удерживая ошибки под контролем. Хорошие жонглёры часто приспосабливаются к плохому броску, регулируя темп и направление последующих бросков, и бросают мячи туда, где видят открытое пространство. Ловля также может быть сделана немного раньше или позже, чем в заданное время, путем схватывания мяча в другой точке на дуге. Умелые жонглёры также могут вносить коррективы в скорость и угол броска. Так что даже если мяч приходится бросать из неудобной позиции, он будет пойман в удобной позиции.
Точное моделирование ошибки будет очень сложным. Путем статистического анализа жонглёра с заданным паттерном можно определить зону ошибки вокруг каждого мяча, в которой мячи могут оказываться с некоторой долей вероятности. Зона ошибки вокруг каждого мяча является нечёткой областью, которая, вероятно, будет изменяться по форме и размеру во время полета мяча.
В последующем анализе постоянная круговая зона ошибки вокруг каждого мяча может быть смоделирована путем простого добавления коэффициента запаса прочности в диаметр мячей (используется значение превышающее фактический диаметр мяча). Пожалуйста, обратите внимание, что неизменная круговая зона ошибки является всего лишь допущением.
Оптимальные дуги
Каждая дуга имеет некоторое среднее количество мячей Ω, которые находятся на ней в любой момент времени. Определим оптимальную дугу как дугу, имеющую минимальные размеры, в которые можно вместить заданное количество мячей. Когда минимальные размеры будут достигнуты, каждый мяч будет касаться ранее брошенного мяча в некоторой определенной точке на дуге. (Обратите внимание, что каждый мяч будет касаться двух других мячей: мяча, брошенного до, и мяча, брошенного после). Поскольку теперь размер мяча имеет значение, определим новую переменную:
D = диаметр мяча
Поскольку горизонтальная скорость брошенных мячей не меняется, горизонтальное расстояние между мячами на одной дуге также является постоянным. Проследите за двумя мячами, последовательно брошенными в моменты времени t и t + τ. Мячи расположены максимально близко в верхней части дуги, когда они находятся на одной высоте, один летит наверх, а другой падает вниз.
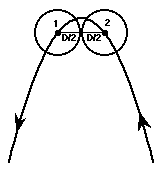
Оптимально, чтобы два мяча только соприкасались в этой точке, поэтому горизонтальное расстояние между их центрами должно быть равно одному диаметру мяча. Поскольку мы уже знаем, что горизонтальное расстояние является постоянным, мы можем написать два простых уравнения, которые я назову оптимальными уравнениями дуги. Эти уравнения будут связывать между собой расстояние полета, скорость и время с размером и средним количеством мячей, которые находятся на оптимальной дуге.
F = Ω*D
Vh = D/τ
Можно заметить, что эти уравнения не зависят от высоты броска. Также можно заметить, что оптимальная дуга должна содержать вершину параболы и должна быть шире минимального горизонтального расстояния D/2 в каждом направлении, поскольку уравнения были получены из того факта, что два мяча могут находиться на одной дуге на одной высоте.
Теоретически, можно кидать по дуге с F < (Ω*D), в том случае, если дуга не содержит вершину параболы, и таким образом уменьшить минимальное горизонтальное расстояние D/2 в каждом направлении. Но, паттерны с подобным типом дуги сложно реализовать на практике, поскольку требуют значительно больших движений и скоростей рук, в сравнении с другими моделями.
Также для паттернов с тремя мячами, где r > 0.5 никогда не бывает больше одного мяча на дуге (Ω < 1). В подобных случаях мячи не могут коснуться друг друга, и, следовательно, к ним не применяется оптимальное уравнение дуги.
Каскад
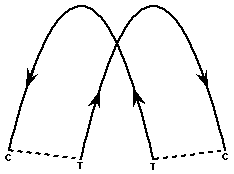
Каскад — наиболее часто применяемый в жонглировании паттерн. В этом паттерне нечётное количество мячей перебрасываются между двумя руками. Руки в ровном ритме попеременно бросают мячи по двум симметричным дугам. Каждая рука бросает мячи вверх рядом с серединой паттерна таким образом, что мячи летят накрест и ловятся с внешней стороны паттерна другой рукой. На протяжении всей этой статьи на диаграммах жонглирования будут отображены позиции броска (throw) и ловли (catch), обозначенные T и C. Перемещение руки между этими позициями представлено пунктирной линией, точная траектория руки не определена.
Немногие жонглёры достигали уровня, на котором могли удерживать каскад девятью мячами. Энтони Гатто, как сообщается, добился удерживания девяти мячей в течении 30 секунд.
прим. переводчика — статья 1996 года, и некоторые сведения устарели. На момент написания перевода (2021 год) рекорд в жонглировании 9-ю мячами принадлежит всё тому же Энтони Гатто, и составляет 53 секунды (253 кетча).
Если запустить каскад в обратном направлении, делая броски снаружи и ловя мячи ближе к середине паттерна, то получается паттерн, называемый обратным каскадом. Он несколько сложнее чем обычный каскад, поскольку точка пересечения в паттерне достигается позже в полете мяча, в результате чего ошибка нарастает в течении более длительного времени до точки пересечения, где наиболее высока вероятность столкновения.
Нахождение минимального расстояния между двумя дугами каскада
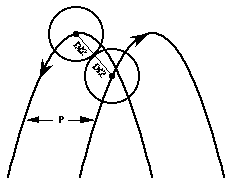
Определим новую переменную:
Р = горизонтальное расстояние между двумя параболическими дугами.
Предположим, что мы жонглируем каскадом мячами с диаметром = D, с двумя дугами, расположенными друг от друга на расстоянии P. Рассмотрим два последовательно брошенных мяча, по одному на каждой дуге. Предполагая, что они коснутся друг друга так, как это изображено на рисунке, можно начать двигаться в обратном направлении, чтобы найти оптимальное значение P.
Исследуем два мяча в момент прикосновения. Движение мячей в этот момент наиболее легко описывается, если использовать систему отсчета нижнего мяча. В подобной системе отсчета нижний мяч неподвижен, а верхний мяч имеет постоянную скорость относительно нижнего мяча.

Поскольку мячи движутся в противоположных направлениях по горизонтали, относительная горизонтальная скорость составляет 2*Vh. По вертикали мячи имеют одинаковое ускорение, g, но поскольку они были брошены с разницей во времени равной τ/2, то относительная вертикальная скорость будет равна g*τ/2. После касания мячи продолжат двигаться пока не окажутся на одной высоте. Поскольку мячи находятся на эквивалентных параболах, расположенных на расстоянии P, горизонтальное расстояние между мячами в этой точке также будет равно P.
Тангенс α можно рассчитать используя простую тригонометрию:
tg(α) = D*(P2 - D2)-1/2 = [(P/D)2-1]-1/2).
Другое уравнение для tg(α) можно записать с использованием относительных скоростей. tg(α) = (относительная вертикальная скорость / относительная горизонтальная скорость) = g*τ/(4*Vh).
Приравняем эти уравнения друг к другу, и решим относительно (P/D). Получаем что:
(P/D) = [(4 * Vh/g/τ)2 +1](1/2).
Далее, принимая, что мы используем оптимальные дуги, можно подставить в это уравнение оптимальные уравнения дуги для P. В результате чего P может быть выражена как функция от периода руки τ и диаметра мяча D (Гравитация, разумеется, является константой):
(P/D) = [(4*D/g/τ/τ)2 +1](1/2).
Вот важные заключения, которые дают данные уравнения:
- Оптимальное значение P не зависит от количества мячей, конечной точки дуги и т. д. Конечные точки дуги (позиции броска и ловли) определяются средним количеством мячей, занимающих дугу. Ω увеличивается по мере того, как конечные движутся вниз, включая бо́льшую часть дуги.
- P/D всегда больше 1. Для человеческих жонглёров, делающих каскад, оптимальное значение P/D обычно очень близко к 1. На деле, оптимальный каскад с P/D > 1,1 очень сложен, поскольку при жонглировании большими мячами потребуется двигаться очень быстро.
Оптимальное расстояние между дугами в каскаде всегда приблизительно соответствует одному диаметру мяча; поэтому даже в каскаде с очень большим количеством мячей, руки могут двигаться на довольно коротком расстоянии. Это преимущество, которое, как мы увидим далее, есть не у всех паттернов.
Оптимальный каскад
Формы и взаимное расположение дуг определяются уравнениями для P и оптимальными уравнениями дуги. Теперь мы должны определить оптимальные конечные точки дуг, в которых будут располагаться позиции броска и ловли. Мы не будем считать, что броски и поимки происходят на одной высоте. Введем новые переменные:
E = расстояние удерживания = расстояние между позициями броска и ловли
θ = угол удерживания

Предположим, что у нас есть две дуги в каскаде, а также значения для Vh, F и P. Мы хотим найти точные позиции броска и ловли на этих параболах, что позволит минимизировать расстояние между броском и ловлей. (В этом месте уравнения начинают становиться довольно путанными, поэтому я просто приведу общий метод и результаты.) Во-первых, находим оптимальное значение θ, для минимизации расстояния удерживания E. Это делается через вычисление уравнения для E в терминах заданных величин и θ, и вычислением производной по θ: dE/d(θ) = 0. Результат:
tg (θ) = 2 * Vh*Vh/g/F.
прим. переводчика — из интереса я решил проверить вывод формулы. Результат совпал. Вывод можно посмотреть на следующих трех фото: 1, 2, 3.
Подставляя это значение обратно в уравнения для E и H, получаем следующее:
E = P * cos(θ).
Что означает — расстояние E по которому должны двигаться руки немного меньше чем P, но при этом E всё равно больше, чем диаметр мяча D. Результат для H:
H = {F + [P*sin(θ)*sin(θ)]}2/[4*F*tg(θ)]
Как упоминалось ранее, если θ мала, то H можно упростить до вида:
H = g * f * f / 8.
Существует предел того, насколько низко можно делать оптимальный каскад. Мячи на одной дуге должны касаться мячей на другой дуге. Предел достигается в момент, когда брошенный мяч касается брошенного ранее с другой руки мяча. Краткое изложение как найти уравнение этого предела. Сначала напишем уравнение расстояния между двумя последовательными бросками из противоположных рук. Установив производную по времени от этого = 0, находим время, на котором расстояние между мячами сведено к минимуму, и, в оптимальном случае, соприкасаются. Задав это время = 0, получим уравнение для паттернов, где мячики касаются в момент броска. Итоговый результат, написанный для полноты:

Для всех пространственно оптимальных каскадов с пятью и более мячами будет применяться уравнение для P и оптимальные уравнения дуги. Каждый мяч будет касаться четырех других мячей во время полета: мячей до и после него на одной дуге, и двух мячей, между которыми он проходит на другой дуге. В оптимальном каскаде с 3 или 5 мячами, каждый мяч касается другого мяча в паттерне.
В случае с каскадом тремя мячами, есть только два других мяча. Так как любые два мяча в каскаде тремя мячами бросаются подряд, то если два мяча где-либо касаются друг друга, то все мячи касаются друг друга, и паттерн является пространственно оптимизированным. Уравнение для P является единственным уравнением, которое потребуется для определения пространственно оптимизированного каскада тремя мячами. Оптимальное уравнение дуги можно применить для каскадов тремя мячами с Ω >= 1, но это ненужное ограничение.
Все эти результаты для пространственно оптимальных каскадов отображаются в прилагаемой к этой статье компьютерной программе Optimal Juggler (только для Macintosh).
Лучшее соотношение удерживания
Какое лучшее значение r? После того, как мяч пойман, рука должна перейти от позиции ловли к позиции броска. И после того как мяч брошен, рука должна сдвинуться на такое же расстояние обратно к положению ловли. Поэтому разумным исходным предположением было бы то, что r = 0,5. Однако, есть несколько причин по которым большое время удерживания может быть выгодно:
- Скорость руки должна соответствовать скорости мяча во время броска. Но чтобы поймать мяч, нам нужно только точно соответствовать позиции, так как мы можем захватить мяч, когда он попадает в руку. Поскольку бросок более ограничен, чем ловля, r должно быть больше 0,5.
- Вес мячей может повлиять на движение руки. В случаях, когда вес мячей не пренебрежимо мал, в течение времени удерживания требуется больше усилий, чтобы поглотить импульс пойманного мяча и придать импульс следующему броску. Поэтому, чтобы помочь свести к минимуму требования к силе рук при жонглировании более тяжелыми объектами, увеличьте коэффициент удерживания r.
- Увеличение r даёт жонглёру больше времени для управления мячом и, следовательно, бо́льшую точность.
- Увеличение r также уменьшает Ω, что может немного снизить вероятность столкновений.
Поэтому наилучшее соотношение удерживания, видимо, находится где-то между 0,5 и 1. Точное значение определяется тем, как жонглёр находит компромисс между точностью броска и легкостью ловли. Если коэффициент удерживания мал, то получаем меньше времени чтобы сделать точных бросок. Если коэффициент удерживания слишком велик, ловля может быть более трудной, так как имеется меньше времени, чтобы добраться до позиции ловли. Различные тесты с высококвалифицированными жонглёрами показывают, что предпочтительный коэффициент удерживания для каскадов с 3, 5, 7 или 9 мячами близок к r = 2/3.
Теоретически оптимальные каскады
Паттерны, описанные ниже, малоприменимы на практике, поскольку могут быть сделаны только при условии бесконечно быстрого жонглирования или при g=0. Хотя я не стал их подробно изучать, есть несколько интересных моментов:
Высота паттерна может быть сколь угодно малой, если дуги не пересекаются. Если опустить H до нуля, дуги становятся горизонтальными линиями. Подобный паттерн с пятью мячами и r = 0 будет выглядеть следующим образом:

С 3 мячами, при Ω < 1, размеры паттерна можно полностью минимизировать, с дугами, фактически сведенным к точкам. F = 0, H = 0, E = D, Vh = 0, Vv = 0.
С пятью или более мячами F может быть уменьшена до нуля, если броски делать вертикально по двум колонкам. Каждый мяч ловится в верхней части одной колонки, а затем бросается в другой колонке. Колонки можно разместить на минимальном расстоянии P=D/sqrt(2). С пятью мячами и r=0 паттерн выглядит следующим образом:

Фонтан
При жонглирования чётным числом мячей наиболее распространенным паттерном является фонтан. Две руки жонглируют независимо друг от друга, по половине мячей на каждую руку. Броски обычно синхронизированы или противоположны по фазе. Как и в каскаде, обе руки бросают от середины наружу.

Поскольку одна и та же рука должна ловить мячи которые она бросает, E = F. Чтобы минимизировать расстояние при бросках, броски и ловли должны делаться на одной и той же высоте. Оптимальное уравнение дуги также применяется ко всем оптимальным фонтанам:
E = F = Ω * D.
Обратите внимание, что расстояние, на которое движутся руки в фонтане, увеличивается пропорционально количеству мячей без конечного предела. Таким образом у фонтана есть минусы при жонглирования большим количеством мячей.
Высота фонтана независима от всех остальных измерений паттерна и может быть сделана сколь угодно малой. Наилучшая высота зависит от предпочтительного значения τ:
H = g*[(τ*Ω)2]/8.
Так как руки жонглируют совершенно независимо, значение P не зависит от всех остальных параметров паттерна. P обычно приблизительно равно ширине плеч.
Поскольку броски в фонтане направлены на внешнюю сторону паттерна (в отличие от каскада, где броски делаются по направлению к середине), рука должна дважды поменять горизонтальную скорость мяча (в каскаде рука меняет горизонтальную скорость мяча только один раз). При этом, между броском и последующей ловлей, руке вообще не нужно менять горизонтальное направление. Поскольку более сложное движение должно быть сделано между ловлей и броском, коэффициент удерживания r, как ожидается, будет больше 0,5, и может быть даже больше чем в каскаде. Однако, по моим наблюдениям, предпочтительный коэффициент удерживания для фонтанов с 4, 6 и 8 мячами близок к r = 2/3, примерно так же, как и в каскаде.
Немногие жонглёры были в состоянии жонглировать восемью мячами в фонтане на протяжении более нескольких циклов.
Асимметричные скрещивающиеся паттерны

Существует довольно большой диапазон возможных асимметричных скрещивающихся паттернов, с различными временными и высотными коэффициентами. Время может варьироваться от синхронного выполнения до противоположного по фазе, руки могут бросать на одну высоту или на совершенно разные высоты, пока получается избежать столкновений мячей в точке пересечения.
Для большого чётного количества мячей, многие жонглёры предпочитают синхронный паттерн, в котором одна рука бросает чуть выше другой, во избежание столкновений посередине. Такой паттерн имеет преимущество перед фонтаном поскольку требует меньших движений рук. Если у жонглёра есть ведущая рука, то он может в большей степени варьировать высоту, и таким образом ведущая рука делает бо́льшую часть работы, в то время как не ведущая рука делает меньше работы.
Асимметричные скрещивающиеся паттерны возможны и для нечётного количества мячей, но они используются довольно редко, поскольку каскад в общем случае проще.
Поскольку руки могут совершать разные движения и разные коэффициенты выдержки, то такие добавочные переменные делают поиск оптимального паттерна намного сложнее, чем для каскадов и фонтанов.
Немногие жонглёры смогли жонглировать восемью мячами в подобном паттерне более нескольких циклов. Bruce Sarafian, как сообщается, сделал 20 кетчей с 10-ю.
Полукаскад

Паттерн полукаскада асимметричен, но точка пересечения отсутствует. Одна рука делает длинные, высокие броски через верх, а другая рука делает более короткие и низкие броски под ней. Данный паттерн выполняется как с нечётным, так и с чётным количеством мячей. Одна рука делает бо́льшую работу, что может быть выгодно для жонглёров с доминирующей рукой. Расстояние между броском и ловлей может быть даже меньше, чем в каскаде.
С различным количеством мячей, соотношение высоты или времен также должно меняться. Как и с другими асимметричными паттернами, различные высоты и времена делают нахождение оптимального паттерна очень сложным.
Теоретически оптимальный полукаскад (возможен, при g = 0 или при бесконечно быстром жонглировании), будет выглядеть так (с 8-ю мячами):

прим. переводчика — мне кажется интересным тот момент, что при рассмотрении полукаскадов с чётным числом мячей если использовать асинхронные сайтсвопы с разницей по "высоте" = 2, например,75для шести мячей, или97для восьми, то получается, что на высокой дуге будет находиться в среднем на два мяча больше чем на нижней, и при этом F для каждой дуги будет оптимальной. А расстояние между позициями броска и ловли также будет близко к оптимальному E вычисляемому как для оптимального каскада (а то и меньше). Не может ли это означать что такие полукаскады могут быть проще в исполнении чем фонтаны? Мировые рекорды говорят об обратном, но лично для меня полукаскад шестью реально проще чем фонтан.
Круг

В круге, одна рука бросает мячи по высокой дуге в другую руку, а вторая рука быстро перебрасывает мячи обратно в первую руку. Данный паттерн может быть использован для любого количества мячей, и временные переменные могут оставаться постоянными. Расстояние удерживания можно сделать очень маленьким. Руки могут иметь различные коэффициенты удерживания.
Высота и скорость высоких бросков для круга с (b) мячами примерно такая же, как и для каскада с (2*b-1) мячами. Так как одной рукой выполняется практически вся работа по удержанию мячей в воздухе, то очень сложно удерживать в круге большое количество мячей. Мало кому удалось успешно выполнить круг семью мечами более одного цикла.
Колонны
Еще один интересный паттерн для одной руки — колонны. Каждый мяч занимает одну колонку и бросается прямо вверх, в то время как рука движется от колонны к колонне, ловя и бросая.

В оптимальном паттерне колонн F = 0, а горизонтальная скорость при броске и ловле также = 0. Нет никаких причин, чтобы расстояние между колоннами было больше диаметра одного мяча, D. Это делает перемещение руки между колоннами максимально простым. Высота броска, H, зависит от предпочтительной скорости броска и может быть сделана сколь угодно низкой.
При жонглировании двумя мячами одной рукой, рука просто перемещается между ними. При числе мячей большем чем два, появляются дополнительные варианты порядка перемещения между колоннами. Рука может начать с одного конца и последовательно переходить к следующей колонне (1,2,3,4, …), после чего сделать длинный переход в конце цикла обратно на первую колонну. Лучшей вариантом, вероятно, было бы начать с одного конца бросая нечётные колонны (1,3,5, …) и возвратиться, бросая чётные колонны (…, 6,4,2). Это минимизирует общее движение руки и не потребует перемещения на более чем на две колонны за раз. Среднее расстояние перемещения руки на протяжении всего цикла будет = [2 - (2 / b)] * D.
В каскаде и фонтане, рука два раза проходит расстояние Е при каждом броске, поскольку ей нужно перейти от положения броска к положению ловли и обратно. В колоннах есть только переход от броска к следующей ловле. Горизонтальное перемещение между ловлей и следующим броском отсутствует. По мере увеличения количества мячей среднее расстояние между бросками в колоннах приближается к конечному пределу 2*D.
В теории, если сделать паттерн трехмерным и расположить колонны по кругу, то можно исключить перемещения более чем на 1 диаметр мяча.
На практике же я никогда не видел, чтобы жонглёры выполняли колонны более чем тремя мячами одной рукой.
прим. переводчика — Toby Walker демонстрировал жонглирование 8-ю булавами двумя руками в колоннах. То есть по 4 булавы в колоннах на каждую руку. Делал он это, правда, недолго. https://youtu.be/_k58bljfsBI?t=428
Жонглирование на отскок
Если жонглировать резиновыми мячами над твердым полом, то можно выполнить любой из ранее описанных паттернов на отскок от пола. Жонглирование на отскок как правило выполняется каскадом.

Жонглирование на отскок требует меньше физических усилий, поскольку мячи не бросаются высоко. Также требуются меньшие движения рук, поскольку расстояние удерживания мяча может быть совсем небольшими и мячи бросаются с меньшими скоростями. Мячи легче поймать, поскольку в верхней части паттерна они летят с наименьшей скоростью. Недостатком же является тот фактор, что при жонглировании большим числом мячей, для того чтобы получить больше времени, может понадобиться встать на стул и т. п. Кроме того, ошибки часто приводят к катастрофическим столкновениям, после которых мячи разлетаются по всей комнате.
Все уравнения для оптимального каскада также применимы для каскада на отскок — но только до точки отскока. Так как никакие мячи не отскакивают идеально, провести полноценный анализ чего-либо после отскока крайне затруднительно.
Рекорд в жонглировании семью мячами на отскок составляет более 20 минут в исполнении Pat'а McGuire'а. Tim Nolan смог удержать 10 мячей в течении несколько циклов в паттерне wimpy.
Выброс (флэш)
Под термином жонглирование обычно подразумевают непрерывный паттерн, в котором каждый раз, когда объект пойман, он бросается обратно вверх. Если жонглёр бросает все мячи один раз в паттерне, а затем ловит их всех, то это называется выброс. С точки зрения мячей в воздухе, выброс — это то же самое, что и жонглирование.
Впрочем, в отличие от непрерывного жонглирования, при выбросе руки не должны постоянно двигаться от положения ловли до положения броска. Например, при выбросе каскада или фонтана, расстояние удерживания мяча E, проходится только один раз, после того как все мячи были выброшены, и до того момента, как все будут пойманы. Это делает выброс значительно проще продолжительного жонглирования.
Большее движение руки потребуется для выброса колонн, где рукам приходится передвигаться на расстояние D между бросками.
Выброс 11 мячей в каскаде выполнили Bruce Tiemann и Bruce Sarafian. Двенадцать мячей — самое большое количество, которое Bruce Sarafian выбросил в асимметричном пересекающемся паттерне.
прим. переводчика — на данный момент Alex Barron выполнил выброс 14 мячами в асинхронном фонтане.
В заключение
Жонглирование ограничено пространственными пределами объектов в воздухе. Размер объектов, диапазон рук жонглёра и точность броска ограничивают жонглёра пространственно. Однако описание оптимальных пространственных моделей — это только первый шаг в определении того, как нужно жонглировать. Необходимо также учитывать временные ограничения на руках и ошибки броска, которые сопровождают их, чтобы найти наиболее удобную скорость жонглирования.
Какой паттерн проще всего? Ответ в основном определяется тем, какой паттерн тренировал жонглёр. Как правило, самые простые шаблоны — те, где обе руки работают одинаково, и все броски одинаковы. Как упоминалось ранее, шаблоны, в которых одна рука бросает выше другой, менее эффективны при удержании мячей в воздухе и приводят к более высокому или более быстрому жонглированию, чем шаблоны, в которых обе руки работают одинаково. Жонглирование мячами в каскаде, фонтане или колоннах приведет к примерно одинаковой высоте рисунка. Вертикальные движения рук также будут примерно одинаковыми для трех моделей. Для большего количества предметов, каскад имеет преимущество перед фонтаном по части меньшего горизонтального передвижения руки. Для колонн также требуется большее движение руки, чем в каскаде, и помимо этого существует недостаток, что броски производятся из разных мест. Поэтому, чтобы жонглировать большим количеством мячей, рекомендуется тренировать каскад.
Еще одно свидетельство преимущества каскада над фонтаном можно увидеть в данных, взятых у одного из лучших жонглёров мира, Энтони Гатто. По факту, у него больше места для ошибок в каскаде 9-ю мячами, чем в фонтане 8-ю мячами. Его расстояние удерживания в фонтане 8-ю мячами составляло около 0,44 м, а в каскаде 9-ю мячами всего 0,34 м. Используя уравнения, которые я вывел, можно произвести вычисления в обратном направлении, чтобы оценить допустимую ошибку в любом паттерне жонглёра. С каскадом 9 мячами Энтони Гатто имел диаметр зоны безопасности мяча около 0,20 м. В фонтане 8-ю мячами диаметр этой зоны составлял около 0,13 м.
Из исследования, проведенного в этой статье, можно дать следующий совет относительно исправления проблемы со столкновениями. При жонглировании более чем тремя мячами столкновения обычно происходят так быстро, что трудно определить, что именно пошло не так. Есть два места, где столкновения наиболее вероятны: столкновения между последовательно брошенными мячами из одной руки или между последовательно брошенными мячами на разных дугах.
Если вы постоянно получаете столкновения в верхней части дуги между мячами на одной дуге, попробуйте увеличить расстояние полета F. Если вы используете фонтан, это также означает увеличение расстояния удерживания E.
Если вы получаете столкновения между мячами вблизи точки пересечения в каскаде, попробуйте увеличить E.
Пытаясь изменить какой-либо параметр, может помочь замедление паттерна, что также увеличивает высоту H. Также может помочь увеличение коэффициента удерживания r, поскольку это немного уменьшает количество мячей в воздухе, и дает больше времени чтобы сделать прицельный бросок.
Как уже упоминалось ранее, я обнаружил, что лучшие жонглёры в мире методом проб и ошибок получают паттерны, которые очень близки к оптимальным шаблонам, описанным в этой статье. Если вы хотите улучшить свою форму жонглирования, я рекомендую получить копию моей компьютерной программы Optimal Juggler (для Macintosh).

Выше представлен вид реального окна программы Optimal Juggler. Программа позволяет легко изменять несколько параметров анимированного жонглирования в соответствии с вашим предпочтительным стилем и отображает, как должен выглядеть оптимальный шаблон в реальной скорости или замедленном движении. На самом деле, увидеть, как выглядит оптимальный шаблон, очень полезно в процессе обучения.
прим. переводчика - Поскольку Macintosh есть не у всех (в том числе у меня), я попробовал воспроизвести функционал программы в кроссплатформенном варианте (в виде скрипта на JavaScript). Выполняемая веб-страница расположена по адресу https://andreyrysh.github.io/. На том же Github расположен и код проекта (если кому-то так будет удобнее) — https://github.com/andreyrysh/andreyrysh.github.io.
Сразу оговорюсь, что программа далека от идеала, и при использовании может вылезти немало багов (хоть и некритичных). В частности, при предельных значениях некоторых переменных часто вылезает неадекватная отрисовка мячей и выявление столкновений.
Приложение — таблицы предпочтительных параметров жонглирования
Следующая таблица предпочтительных частот жонглирования была измерена в живую или через видеозапись. Все данные были взяты из того, что казалось стабильным, удобным. (Частоты никогда не следует измерять во время выступления, особенно под музыку, так как ритм музыки может повлиять на скорость жонглёра.) Все жонглёры использовали каскады для нечётных чисел и фонтаны для чётных чисел, если не указано иное.
| # balls (жонглёры использовали привычный им реквизит — размеры и вес отличались) | Предпочтительное τ (секунды) |
| 3 | 0,47 - R. Rubenstein (1994) 0,54 - J. Kalvan (1994) 0,62 - B. Olson (1994) |
| 4 | 0,53 - J. Kalvan (1994) |
| 5 | 0,46 - R. Rubenstein (1994) 0,49 - J. Kalvan (1994) 0,50 - B. Olson (1994) |
| 6 | 0,47 - J. Kalvan (1994) |
| 7 | 0,40 - D. Bennett (1984) 0,44 - D. Tison (1987) 0,44 - A. Gatto (1989) |
| 8 | 0,31* - D. Bennett (1984) 0,38 - A. Gatto (1989) |
| 9 | 0,30 - D. Bennett (1984) 0,33 - A. Gatto (1989) |
* скрещивающийся паттерн с 8-ю мячами.
Следующие средние измерения были сделаны с видеокассет:
| # balls | H | E | F | τ | r |
|---|---|---|---|---|---|
| 3 (D = 7,5 см) (Jack Kalvan) | 0,33 m | 0,20 m | 0,33 m | 0,55 s | ~0,63 |
| 4 (D = 7,5 см) (Jack Kalvan) | 0,65 m | 0,25 m | 0,25 m | 0,53 s | ~0,68 |
| 5 (D = 7,5 см) (Jack Kalvan) | 1,0 m | 0,24 m | 0,39 m | 0,47 s | ~0,68 |
| 6 (D = 7,5 см) (Jack Kalvan) | 1,5 m | 0,38 m | 0,38 m | 0,47 s | ~0,71 |
| 7 (D = 7,5 см) (Jack Kalvan) | 1,8 m | 0,47 m | 0,48 m | 0,42 s | ~0,69 |
| 7 (D = 6 см) (Anthony Gatto) | 1,7 m | 0,37 m | 0,65 m | 0,44 s | ~0,68 |
| 8 (D = 6 см) (Anthony Gatto) | 2,2 m | 0,44 m | 0,44 m | 0,38 s | ~0,63 |
| 9 (D = 6 см) (Anthony Gatto) | 2,2 m | 0,34 m | 0,68 m | 0,33 s | ~0,63 |
Ссылки на литературу
- Airborne! - Highlights of the 1989 International Jugglers Association Convention (1989), New York: IJA / Maverick Media
- Beek, Peter Jan (1989), Juggling Dynamics, Amsterdam: Free University Press.
- Buhler, Joe; Graham, Ron (1984), Fountains, Showers, and Cascades, The Sciences, vol. 24, pp. 44-51.
- Donner, Marc D.; Kalvan, Jack (1988), Recent Progress in Juggling Robot Research, IBM Research Report, Yorktown Heights, NY.
- Lewbel, Arthur (1987-94), The Academic Juggler, Juggler's World:
Memorable Tricks and a Numbers Formula, Winter 1987-88, p. 31.
A Short Lesson in Thought and Gravity, Summer 1988, p. 31. - Magnussson, Bengt; Tiemann, Bruce (1989), The Physics of Juggling, The Physics Teacher, pp. 584-588.
- Shannon, Claude E. (1993) Scientific Aspects of Juggling in Claude Elwood Shannon Collected Papers, edited by N. J. A. Sloan and A. D. Wyner, New York: IEEE Press. pp. 850-864.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Последние комментарии