Addicted to Ball and Club Juggling. Изучаем теорию. Уроки 11-14.
Часть 4. Знание — сила, или теории, факты, концепции.
Урок 11. Что такое теория сайтсвопов, и зачем её нужно учить?
Теория сайствопов это что-то вроде нот в музыке для жонглёров. Конечно, для того чтобы жонглировать совершенно нет необходимости знать теорию, но она может существенно помочь. Может показаться скучным учить теорию в своё свободное время, но я могу пообещать, что эта теория не такая скучная как другие, и, к тому же, она довольно простая. Чтобы убедить в полезности дальнейшего чтения, я приведу несколько аргументов.
И поскольку важно хотя бы немного понимать сайствопы, в конце приведены несколько очень полезных практических упражнений. Что-то вроде уроков в стиле "учитесь-в-процессе".
Во-первых, теория сайтсвопа была разработана чтобы находить новые паттерны. А значит, можно самостоятельно придумывать паттерны. Потенциально возможное количество новых паттернов выходит за рамки нормы. Например, если рассматривать только асинхронные (без одновременных бросков с обеих рук) паттерны без стилевых обработок (то есть без миллс месса, бросков из-за спины, обводок…) и мультиплексов (когда из руки за раз бросается более одного мяча), и с ограничением высоты в 9 (высота для жонглирования 9-ю мячами), то можно обнаружить около 29000 паттернов для четырех мячей. Конечно, большая часть будет выглядеть как полное дерьмо. Но всё равно останутся более тысячи интересных четырехмячиковых паттернов, которые могут быть выполнены в различных стилях и вариациях таких как бэккросы, обводки, миллс месс…
Во-вторых, теория сайтсвопа расширяет понимание паттернов жонглирования. Например, вполне возможно выполнить трюк Burke’s Barrage с тремя мячами без полного осознавания, что именно происходит. Но что если захочется выполнить Burke’s Barrage с четырьмя мячами, или если захочется сделать его с булавами?
В-третьих, невозможно объяснять сложные трюки в текстовом виде без использования нотации сайтсвопа. Даже если и возможно, то объяснение будет крайне громоздким.
В-четвертых, данная теория применяется ко всем видам жонглирования. Мячи, кольца, булавы, перекидки, на отскок, мультиплексы… сайтсвопы используются везде.
В-пятых, она способствует улучшению некоторых трюков. Таких, которые ты уже умеешь делать, но не очень хорошо. Одно небольшое замечание поможет делать полукаскад с четырьмя мячами чисто асинхронным, если одна рука будет бросать на высоту 5 а другая на высоту 3, а не на 5 и 4, как это обычно получается.
В-шестых, выявляет многие паттерны, которые полезны для изучения более сложных трюков. Пять мячей могут быть выучены через паттерны с больши́м числом 5-ок. 55500, 50505, 552, 5551 могут оказаться весьма полезными.
В-седьмых, это способ общения между жонглёрами. В журналах и интернете можно найти много идей, большинство из которых объясняются на языке сайтсвопа.
В-восьмых, это поддержка памяти. Новые придуманные трюки легко забываются. Если удастся записать их, то не понадобиться тратить часы жонглирования, чтобы прийти к трюку, который уже однажды делал.
Надеюсь, что я убедил тебя в полезности изучения теории сайтсвопа. Я действительно надеюсь.
Многие жонглёры не любят сайтсвопы. И тому есть несколько причин. Некоторые не любят комбинацию теории и жонглирования. Другие считают, что теория сайтсвопа недостаточно хороша, поскольку она не может описать всё, и потому что она ничего не говорит о миллс мессе или мультиплексах. Эти аргументы давно в прошлом. Сайтсвоп довольно молодая "наука", и, конечно, не покрывает все проблемы разом, но она довольно быстро развивается. Существуют дополнения теории для описания мультиплексов, миллс месса… дополнения будут приведены в соответствующих описаниях трюков.
Теория сайтсвопов показывает то, что в принципе возможно, но всегда будет оставаться поле деятельности для жонглёров, желающих разрабатывать новые трюки, как интересные, так и возможные.
Урок 12. Краткая теория и упражнения
В этом уроке я собираюсь дать максимально короткое объяснение теории. Оно не будет полностью корректным, и будет касаться только асинхронных паттернов, без мультиплексов, стилей,… Это все будет, но позже, а пока начнем с чего попроще.
Паттерн записывается как строка цифр, в которой каждая цифра обозначает высоту броска.
Например: 534 (читается как "пять три четыре", а не "пятьсот тридцать четыре).
Высоты бросков будут примерно такими:
0 = пустая рука в течении одного такта = "дырка"
1 = быстрый переброс мяча из одной руки в другую = передача, как в круге
2 = удерживание мяча в течении одного такта = пауза
3 = небольшой бросок из руки в руку, как при жонглировании тремя мячами
4 = бросок в ту же руку, как при жонглировании четырьмя мячами
5 = высокий бросок из руки в руку, как при жонглировании пятью мячами
6 = …
Короче, чётные цифры это броски прямо вверх, а нечётные цифры — броски из руки в руку.
Каждый паттерн должен полностью соответствовать следующим правилам:
среднее арифметическое от чисел = количество используемого реквизита
Броски в паттерне делаются на соответствующие высоты, попеременно правой и левой рукой
Пример: среднее арифметическое от 534 равняется 4 (среднее арифметическое = сумма всех чисел, разделённая на количество чисел. В данном примере (5+3+4)/3 = 4). Так, при жонглировании 4-мя мячами можно сделать высокий бросок из правой руки в левую, затем низкий бросок из левой в правую, после бросок вверх правой рукой, высокий бросок слева направо, низкий бросок справа налево, и бросок прямо вверх левой…
прим. переводчика — короче, это выглядит вот так:
И вообще, рекомендую скачать JugglingLab
А сейчас давай пожонглируем. Возьми три мяча. Попробуй выполнить следующие паттерны по порядку. Перед тем как начать делать очередной паттерн, подумай сколько реквизита потребуется. Затем, попробуй понять, что именно нужно сделать, а затем сделай это. Ритм бросков как при обычном жонглировании, но может быть чуть быстрее или медленнее. Заметь, что такой ритм намного быстрее, чем реально успеваешь думать. Так что сперва подумай, что именно нужно сделать, и только затем делай. Также поможет тренировка паттерна бросок за броском. Сначала сделай только первый бросок, потом первый и второй, затем первые три броска…
Представь, что ты смотришь на паттерн, затем осознаешь, что нужно сделать, а затем пробуешь его выполнить. Не заглядывай сразу в описание. Постарайся представить, как должен выглядеть трюк исходя только из его сайтсвопа, и делать его до тех пор, пока он не начнет получаться достаточно уверенно. Только после этого загляни в описание.
- 31
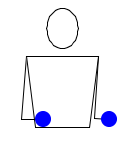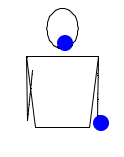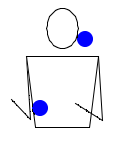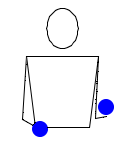
Жонглирование 2-мя мячами. Правая рука бросает мяч налево, а левая быстро перебрасывает второй мяч направо. Правая рука ловит мяч с левой, левая ловит мяч с правой. Затем все повторяется в таком же ключе: правая рука бросает, а левая перебрасывает. Аналогичные паттерны, в которых одна рука все время делает переброс, также называются кругами. (другие круги: 5111, 51, 7131, 717111, 71…)
- 312
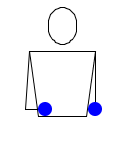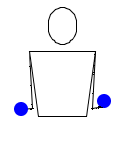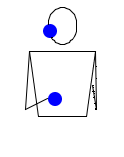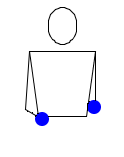
И снова два мяча. Начало аналогично предыдущему, но затем, вместо того чтобы продолжить бросать, правая рука берёт паузу, после которой уже левая рука начинает с броска, а правая делает переброс,…
Если паттерн имеет нечётное число бросков, то это всегда означает смену рук. Таким образом паттерн становится симметричным и более красивым, но и более сложным. - 411
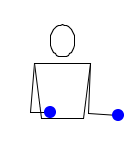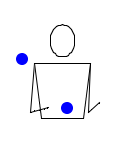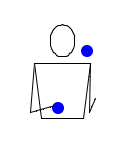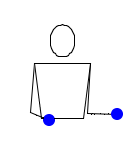
Опять два мяча. Правая рука бросает мяч прямо вверх. Сразу после этого левая рука перебрасывает второй мяч в правую, а правая рука тут же перебрасывает этот мяч обратно. Левая его ловит, и только после этого правая рука ловит первый высоко брошенный мяч. Затем тоже самое, но на другую сторону. Делай всё быстро. Ни в один момент времени в одной руке не должно оказаться двух мячей. Пока один мяч находится в воздухе, второй мяч перебрасывается из руки в руку и обратно.
- 4233
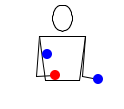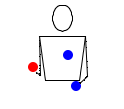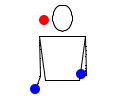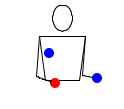
Смотри-ка, три мяча. Данный паттерн представляет из себя каскад тремя мячами, но после двух бросков, один мяч бросается вверх, следующая рука ничего не делает, а затем все повторяется сначала.
Если у тебя получилось, попробуй также сделать 423 и 42333.
Так как 4233 имеет чётную длину, то смены рук не происходит. Для тренировок симметричных паттернов можно (как правило) добавить базовую высоту (для трех мячей это 3), и отработать для начала несимметричный паттерн. (так 4233 помогает выучить 423 и 42333) - 501
Снова два мяча. Это упражнение потребует некоторой сноровки. Так как второй бросок это ноль, левая рука должна быть пустой (это не совсем так работает, долго объяснять… будет рассмотрено далее в теории состояний). Так что начни с двух мячей в одной руке. Далее нужно делать всё быстро. Очень быстро. Высокий бросок в пустующую руку, затем переброс в ту же руку, а теперь, прежде чем поймать высоко брошенный мяч, сделай только что пойманным мячом высокий бросок в обратном направлении, поймай первый брошенный мяч и перебрось его в том же направлении… Если не получается, бросай выше и быстрее, до тех пор пока этот паттерн не начнет странным образом удерживаться в воздухе.
прим. переводчика — более подробное описание трюка можно почитать и посмотреть в уроке по 531 - 52512
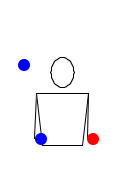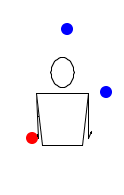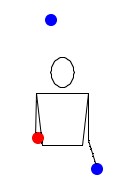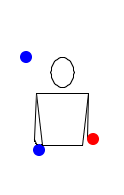
Последнее упражнение в этом уроке. Если получится его отточить, значит ты сможешь понять любой паттерн. Высокий бросок справа налево, затем опять тоже самое, переброс из левой руки в правую, поймай и брось обратно высокие броски слева направо, затем переброс справа налево, поймай высокие броски и опять брось их назад…
Вот еще несколько простых паттернов, которые можно попробовать: 41401, 5111, 522, 4413, 4512 и 55113
Если сможешь сделать и эти паттерны, то поверь мне, ты можешь претворить в жизнь любой базовый паттерн, и единственное, что потребуется для реального жонглирования — тренировки. Это на самом деле так, я абсолютно серьезен. Всё имеющее отношение к сайствопам и теории жонглирования на 95 процентов предназначено для нердов-теоретиков. Впрочем, оставшиеся 5 процентов могут оказаться довольно интересными…
Урок 13. Длинный рассказ об асинхронных сайтсвопах
В теории сайтсвопов (СС), для упрощения системы, паттерны уменьшены до предела. Как писалось в предыдущем уроке, если бросать попеременно с правой и левой руки, то цифра обозначает количество тактов/счётов, которые мяч проведет в воздухе, и этого достаточно, чтобы понять, что именно надо делать. Это число счётов называется "высотой" броска.
(1) на самом деле, цифра обозначает число тактов до того как мяч будет брошен снова, то есть цифра скорее обозначает количество тактов в воздухе + 1. По это причине в число счётов также входит бросок предмета после кетча.
Чётные броски прилетают в ту же руку, из которой были выброшены.
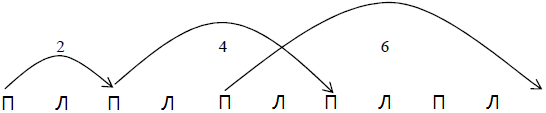
Нечётные броски перелетают из одной руки в другую.

Как же бросать на эти высоты?
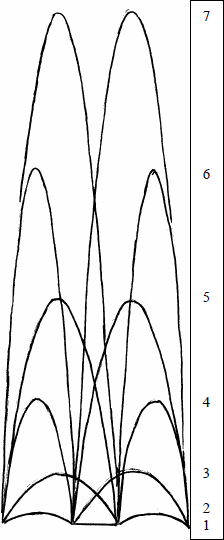
Поскольку высота на самом деле это время/число тактов, то реальная высота будет зависеть от скорости жонглирования. Однако соотношение высот всегда остается одинаковым (если только не меняется время удерживания и тому подобное).
Если мяч проводит в воздухе в два раза дольше времени чем другой, то высота его броска намного больше чем в два раза. Например, 6 значительно выше чем удвоенная высота 3 (легко выводится из формулы: реальная высота = Сv × (высота - время удерживания)2).
На диаграмме справа показано, как высоты бросков соотносятся между собой. Впрочем, точная высота каждого броска зависит от скорости жонглирования. Чем быстрее жонглируешь, тем ниже должны быть броски — т.н. редукция высоты.
В прилагающаяся таблица приведены соотношения между бросками (время удерживания = 1,3 время ожидания = 0,7)
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|
| 3 | 2,5 | 4,7 | 7,5 | 11 | 15 | 20 | 26 |
| 4 | 1 | 2 | 3 | 4,5 | 6 | 8 | 10 |
| 5 | 1 | 1,6 | 2,4 | 3,3 | 4,3 | 5,5 | |
| 6 | 1 | 1,5 | 2 | 2,7 | 3,5 | ||
| 7 | 1 | 1,4 | 1,8 | 2,3 | |||
| 8 | 1 | 1,3 | 1,7 | ||||
| 9 | 1 | 1,3 |
Не так-то просто определить сделан бросок только в 2 или в 4,7 раз выше.
Для начала попробуй следующее:
Мячи и кольца
Если ты не умеешь жонглировать четырьмя мячами, то стоит рассматривать только высоты до 5. И если у тебя возникают трудности, то как правило для решения проблем достаточно увеличить разницу между высокими и низкими бросками( и/или увеличить скорость).
Если же есть навык жонглирования четырьмя мячами, то могут помочь следующие упражнения:
Высота 3: быстрый каскад тремя мячами. Все проблемы возникают из-за того, что 3 бросается слишком высоко. Для паттернов в которых один мяч бросается высоко вверх, с последующими несколькими низкими бросками (например 633), намного важнее бросать низкие, быстрые 3-ки, чем делать стараться делать высокие броски еще выше.
Высота 4: низкий фонтан четырьмя мячами.
Высота 5: кидая асинхронный фонтан четырьмя мячами, кинь один мяч выше (примерно в два раза) и прямо. Если после этого получился чёткий переход в синхронный паттерн, то значит это была высота 5. Также можно несколько скорректировать высоту, ловя мяч чуть выше или ниже. Вполне естественно стремление поймать брошенную 5 немного выше (раньше) чем обычно, и таким образом можно остаться в асинхронном паттерне. Так что будь в курсе, что такое возможно, и сделай наоборот если ты хочешь перейти в синхронный фонтан. (так же убедись, что другой бросок остается на обычной для 4-ки высоте). прим.переводчика — в записи сайствопа такой трюк будет записан как 4445x41x(4,4)(4,4)(5x,4)(1x,4)!(4,0)!
Высота 6: брось еще выше. Таким образом ты останешься в синхронном или асинхронном паттерне. прим.переводчика — 44444642 или, в синхронном варианте, (4,4)(4,4)(6,4)(2,4)
Высота 7: Брось еще выше и перейди в синхронный паттерн(асинхронный) прим.переводчика — 4447x4241x(4,4)(4,4)(7x,4)(2,4)(1x,4)!(4,0)! — выглядит, возможно, жутковато, но это из-за длины паттерна и обилия скобок и запятых. На самом деле всё не так страшно.
…
прим.переводчика — на мой взгляд, все приведенные выше упражнения удобнее выполнять начиная с синхронного паттерна, с последующим переходом в асинхронный (или все в тот же синхронный, если речь идет о чётных бросках). Также, возможно стоит добавить, что после высокого броска с одной руки, вторая продолжает кидать 2 в 1. Чем выше бросок, тем больше дополнительных бросков делается в ожидании прилёта высоко брошенного предмета.
Булавы
"Булависты" с трудом согласились, что теория сайтсвопа интересна. И тому было несколько причин. Нотация сайтсвопа не говорит как должен быть сделан бросок. Если мяч летит, то он просто летит. А булавы могут летать разными путями. И именно эти вариации броска делают жонглирование булавами интересным. К тому же сайствопы наиболее полезны при жонглировании более чем тремя предметами, в то время как c булавами броски на высоту четырех или пяти булав не являются простыми.
Тем не менее, теория всё равно остается достаточно интересной, чтобы изучить её (например, для использования в паттернах для перекидок). К тому же всё больше и больше булавистов начинают делать сайтсвопные паттерны.
В общем случае будет правильно считать так:
- 3 — обычный бросок на один оборот
- 4 — бросок на два оборота
- 5 — три оборота
- 6 — четыре оборота
Но в простых, более элегантных или быстрых паттернах как правило наблюдается уменьшение числа оборотов. Пять булав, например, обычно кидаются на два оборота, поскольку три оборота рассчитаны под скорость обычного каскада тремя булавами. И, конечно, пятью булавами возможно жонглировать быстрее. В общем, пять булав часто кидаются на два оборота. При медленном вращении итоговый паттерн выглядит более элегантно, да и на два оборота кидать проще.
С учётом уменьшения числа оборотов получаем следующее:
- 3 — быстрый один оборот
- 4 — медленный на один оборот
- 5 — медленный на два оборота
- 6 — медленные три оборота или очень медленные два оборота
- 7 — очень медленные три оборота
(Подробнее написано "Part Two Chapter 2: basic patterns" на 104 странице.)
В каком случае последовательность цифр возможна для жонглирования?
Паттерн будет работать только в том случае, если он будет соответствовать двум правилам:
Правило 1
Среднее арифметическое цифр строки соответствует числу предметов, которым надо жонглировать
Если ср.арифм. будет равно 3,33, то конечно же данный паттерн будет невозможен для жонглирования. Например, паттерн 334 невозможен ((3+3+4)/3=3,33). В то время как 3342 уже будет реален ((3+3+4+2)/4+3), и представляет из себя жонглирование тремя предметами.
Правило 2
Два предмета никогда не прилетают одновременно
Это довольно просто понять. В независимости от того насколько хорошо ты жонглируешь, всегда будет необходимость в коррекции бросков перед тем как поймать мяч. Если два мяча прилетают одновременно, то не получится поймать два мяча сразу. (Разумеется, если очень хочется, то это можно сделать. В качестве примера можно привести некоторые элементы Люка Бэрриджа, но по большому счёту вряд ли захочется чтобы такое происходило (как и вряд ли захочется быть похожим на Люка Бэрриджа) )
Проверить не прилетают ли два мяча одновременно можно несколькими способами.
Можно прибавить к каждому броску его порядковый номер. Если все числа получаются разными, значит они прилетают в разные моменты времени
Пример
3333 превращается в 3+0 3+1 3+2 3+3 = 3456, таким образом 3333 корректен.
342 превращается в 3+0 4+1 4+2 = 354, таким образом 342 корректен.
432 превращается в 4+0 3+1 2+2 = 444, таким образом 432 некорректен.
405 превращается в 4 1 7 7 4 10, таким образом 405 некорректен.
прим. переводчика — в последнем расчёте может возникнуть вопрос: "а почему это рассматривается длина паттерна равная шести (405405), когда во всех примерах выше рассматривалась только оригинальная длина паттерна?" Причем, если рассматривать одиночную длину, то получаемый результат 417 не имеет столкновений. Ответ прост: в (405 задействуются три мяча (4+0+5/3=3), но в первых трех бросках кидаются только два мяча, а вот если кинуть еще один мяч (во втором периоде), то сразу же будет выявлено столкновение. В общем, имхо, излишне замороченный метод, и не особо удобный для быстрой проверки. Я бы порекомендовал присмотреть какой-нибудь метод из приведённых здесь.
Второй метод по сути аналогичен: нарисуйте стрелки соединяющие броски с местами приземлений. Две стрелки никогда не должны приходить в одно место прим. переводчика — за исключением мультиплексов.
Пример
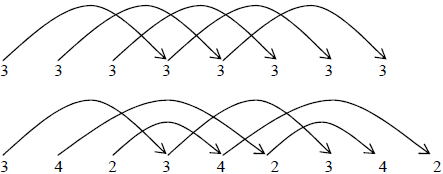
Специальные пометки
Запись 42(3) означает следующее: сделать 42 (два в одной руке) один раз, а после продолжить каскад тремя
[43]23 — мультиплексный паттерн. Более подробно изложено в 5-м уроке (стр. 25) и 6-й главе во второй части (стр. 169).
Дополнительные правила
Данные правила не являются необходимыми, но всё равно будет полезно их знать. Они могут поспособствовать пониманию красоты паттернов, и, таким образом, сэкономить время.
- В паттернах с нечётной длиной происходит смена рук (симметричны). Для паттернов с чётной длиной это не так
После того как паттерн с нечётной длиной был выполнен один раз, первый бросок второго выполнения паттерна будет сделан рукой, отличной от той с которой он был начат.
Пример: 441 будет выполняться следующим образом:
4 правой 4 левой 1 правой 4 левой 4 правой 1 левой Таким образом бросок на каждую высоту будет выполняться обеими руками. Из-за этого подобные паттерны сложнее в исполнении, но и более красивы. Для тренировки может быть полезно сначала отработать паттерн с чётной длиной. Для этого добавьте один бросок базовой высоты (высота равная числу мячей, которым происходит жонглирование)
- Длинные паттерны сложны для исполнения и, как правило, не особо привлекательны, если только не имеют чёткой визуальной структуры
Отличный длинный паттерн с тремя мячами — 3456012. Зрители видят 0123456, т.е. мячи взлетают выше и выше, накидываясь на одну руку.
- Если прибавить (или вычесть) длину паттерна к одному из бросков, то получается корректный паттерн в котором задействуется на один предмет больше (меньше)
Так, 441 можно перевести в 741, 444 или 471.
Данное правило довольно полезно для нахождения паттернов, которые были бы похоже на те, что хочется выучить, и в то же время были бы более простыми. - Если прибавить 1 к каждому броску, то получается новый паттерн, но с добавлением одного предмета
Например, всё тот же 441 превращается в 552.
- Если предмет бросается на высоту равную длине паттерна, то этот бросок всегда будет делаться одним и тем же предметом.
Очень полезное правило. Помогает в изучении трюка или для понимания увиденного паттерна.
Если один мяч постоянно бросается на одни и те же две высоты, то значит, что сумма эти высот равна длине паттерна
На сцене такие паттерны отлично смотрятся, если один мяч окрашен в другой цвет.
Например: 4413, 531, 52233, 534, 53444, 633, 6334, 7333444…Это правило удобно использовать для несколько-уровневых кругов.
Например:
7131 — 13 кидается одни и тем же мячом, поскольку 1+3=4=длине паттерна
51517131 — 17 кидается одним и тем же мячом
915171 — 15 кидается одним и тем же мячом
Упражнения: несколько вопросов
Какие паттерны невозможны для жонглирования?
914, 333423, 881, 801, 741, 432, 63, 55561551, 8441841814414
Ответ:
914, 881, 432 и 63 некорректны
Исправь, чтобы они стали возможными
Например:
914 невозможен, но 714 и 915 уже возможны. Отметь, что 924 и 951 не являются возможными.
Во сколько раз 4 выше чем 3?
Тот же вопрос для 5 и 4, 6 и 4, 9 и 5.
Урок 14. выбор паттернов. Красота и сложность
Красота паттернов
При самостоятельном поиске паттернов, неплохо бы знать как они будут выглядеть до того как начать их тренировать. По-хорошему тут нужно уметь чувствовать паттерн, но я могу дать несколько общих правил, которые могут помочь. прим. переводчика — разумеется, в настоящее время существует такой замечательный способ как "посмотреть в JugglingLab'e", но иногда и он даёт сбой.
- Нули
Паттерны с нулями/"дырками" в большинстве своем выглядят странно, не плавно, безобразно (но уродство может быть полезным). Нули могут быть полезны в качестве подводящих упражнений, или для того, чтобы сделать пируэт или что-либо в этом духе.
- Двойки
За небольшим исключением, паттерны с наличием пауз не отличаются привлекательностью. Но в то же время, если использовать паузу, чтобы сделать что-нибудь, то паттерн становится очень интересным.
- Длинные паттерны
Длинные паттерны (больше 5 бросков) будут красивы только в случае легко распознаваемой структуры; если получается своего рода чёткая картинка. Во всех остальных случаях зрители будут наблюдать непонятную мешанину бросков.
Примеры:
3456012 — мячи летят выше и выше. Выглядит как 0123456 0123456 …
7272715 — три мяча кидаются по одной дуге, а один мяч перебрасывается из руки в руку
97531 — мячи брошенные накрест достигают верхней точки в один момент, образуя великолепную радугу
6461641 — используются только три различных высоты. Смотрится как игра с низкими и высокими вертикальными броскамиДля коротких паттернов подобной проблемы не возникает
- Чётные и нечётные паттерны: симметрично или нет.
Нечётныe паттерны, это паттерны с нечётным числом бросков. В нечётных паттернах броски чередуются и выполняются с обеих рук, что смотрится очень красиво. В чётных паттернах смены рук нет, что облегчает выполнение паттерна. Чтобы сделать паттерн чётным или нечётным (для паттернов с базовым состоянием) достаточно просто добавить бросок на базовую высоту.
Например:
441 — руки чередуются. Легче выучить 4413 (3 потому что это паттерн с тремя мячами), в котором руки не меняются.
5551 — руки не чередуются. Будет замечательно, если удастся добавить 4 (т.к. 5551 — 4-х предметный паттерн). Т. о. получаем 55514.
прим. переводчика — хотя тут не обходится без исключений. Например, 51, 71, 9151, 7333 прекрасно смотрятся, несмотря на свою "чётность".
Сложность паттернов
При обнаружении паттерна, который выглядит достаточно интересно, неплохо бы знать насколько он будет труден в исполнении. Есть несколько логичных правил, которые могут помочь оценить сложность.
- Чем больше предметов, тем сложнее (а то бы ты не догадался!)
- Чем выше броски, тем сложнее
Например: 7333 сложнее чем 6334 - Нечётные паттерны (с нечётной длиной) сложнее чем чётные паттерны
Например: 531 сложнее чем 5313 - Длинные паттерны сложнее чем короткие
Например: 84418414814414 тяжелее чем 84413 - Паттерны с возбуждённым состоянием сложнее чем паттерны с базовым состоянием (подробнее в следующей главе)
Например: 714 и 741 сложнее чем 7441. - Наличие броска 2 упрощает паттерн
Например: 423 проще чем 441, 552 проще чем 534. - Трудны для исполнения сочетания очень высоких и низких (3 или 4) бросков
Например: 813, 633, 933, 834, 73, 73734… - Всегда сложно сделать два последовательных высоких броска
Например: 663 намного сложнее чем 744 - Высокий чётный бросок после низкого нечётного вызывает столкновения (за исключением случаев, когда чётный бросок делается с внешней стороны)
Например: 567801234, 561, 855, 645…
Данные правила могут помочь только примерно оценить сложность, все же у каждого паттерна своя собственная история. В уроке 19: теория стабилизации, можно найти добавочные сведения по оценке сложности паттерна.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Наверное, сайтсвапы - это полезно. Но это совершенно невозможно выучить.